Некоторые линейные операторы
Оператор А, действует в пространстве C[a,b], в котором расстояние между функциями определяется следующим образом:
p (fn(t), f0(t)) = ![]() | fn(t) - f0(t)|.
| fn(t) - f0(t)|.
Решение:
p (A fn(t), Af0(t)) = ![]() |
|-
 |.
|.
| -
-  | = |
| = | |
| ![]()

![]()
 = p (fn(t), f0(t))
= p (fn(t), f0(t)) ![]() = p (fn(t), f0(t)) (x-a)
= p (fn(t), f0(t)) (x-a) ![]() 0
0
a![]() x
x![]() b.
b.
Таким образом p (A fn(t), Af0(t)) ![]() 0. следовательно по определению 2 оператор А непрерывен.
0. следовательно по определению 2 оператор А непрерывен.
4) Непрерывный оператор является ограниченным (теорема 3):
| |
| ![]() |
|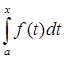 |
| ![]() |
| |
|
| | = 0; |
| = 0; | | = |b-a|.
| = |b-a|.
0 ![]() |
|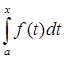 |
| ![]() |b-a|.
|b-a|.
5) Оператор А ограниченный, следовательно у него можно найти норму. Найдем норму оператора А (используя определение ||A||=![]() |A(f)|):
|A(f)|):
||A|| = ![]() |A(f)| =
|A(f)| = ![]() |
|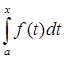 |
| ![]()
![]()

![]()
![]()
 = (x-a);
= (x-a);
a ![]() x
x ![]() b;
b;
Норма оператора А: ||A|| = (b-a);
6) Обратимость интегрального оператора и его спектр.
Возьмем пространство S = {f ![]() C[0,b] / f(0) = 0} с нормой ||f|| =
C[0,b] / f(0) = 0} с нормой ||f|| = ![]() |f(x)|.
|f(x)|.
В пространстве S рассмотрим оператор А:
Аf = 
x ![]() [0,b], t
[0,b], t ![]() [0,x];
[0,x];
Найдем оператор обратный к (A - ![]() *I),
*I), ![]()
![]() R;
R;
(A - ![]() *I)*f = g
*I)*f = g
 -
- ![]() *f(x) = g(x) (1)
*f(x) = g(x) (1)
Пусть функции f и g дифференцируемы;
Продифференцируем уравнение (1), получим:
f - ![]() *f/ = g/ (2)
*f/ = g/ (2)
Это уравнение (2) – дифференциальное неоднородное линейное уравнение. Решим это уравнение, используя метод Бернулли.
![]() - f/ =
- f/ = ![]()
![]() -
- ![]() + f/ = 0 (3)
+ f/ = 0 (3)
Представим решение уравнения в виде: f(x) = U(x)*V(x), тогда уравнение (3) примет вид:
![]() -
- ![]() *U*V + U/ *V + U*V/ = 0
*U*V + U/ *V + U*V/ = 0
U/ *V + U*V/ - ![]() *U*V = -
*U*V = - ![]()
U/ *V + U*(V/ - ![]() *V) = -
*V) = - ![]() (4)
(4)
Решаем однородное линейное уравнение:
V/ - ![]() *V = 0
*V = 0
V/ = ![]() *V
*V
![]() =
= ![]() *V
*V
![]() =
= ![]()
LnV = ![]() + c
+ c
V = ![]() *
*![]() , пусть
, пусть ![]() = с1
= с1
V = с1*![]()
Подставим частное решение однородного уравнения в уравнение (4) при условии, что V/ - ![]() *V = 0.
*V = 0.
Получим уравнение:
U/ * с1*![]() = -
= - ![]()
![]() = -
= -
![]() = -
= - ![]() *
*
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
