Некоторые линейные операторы
Итак:
||Bg|| ![]() ||g(x)||*(
||g(x)||*( ![]() +
+ ![]() *
*![]() {1,
{1, ![]() }*b);
}*b);
То есть В – ограничен.
Остал
ось проверить, что В – оператор, обратный к (A - ![]() *I).
*I).
Если это так, то произведение этих операторов равно единичному оператору или же (A - ![]() *I)*(Bg) = g(x).
*I)*(Bg) = g(x).
Итак, нужно доказать, что
 + g(x) +
+ g(x) + ![]() *
* = g(x)
= g(x)
или
-![]() *
* -
- ![]()
 +
+ ![]() *
*![]() *
* = 0; (*)
= 0; (*)
Возьмем производную от левой части (*) и получим:
-![]() *g(x) -
*g(x) - ![]() *
*![]() *
* +
+ ![]() *
*![]() *
* +
+ ![]() *
*![]() *
*![]() * g(x) = -
* g(x) = -![]() *g(x) +
*g(x) + ![]() *g(x) -
*g(x) - ![]() *
*![]() *
* +
+ ![]() *
*![]() *
* = 0;
= 0;
Следовательно, выражение (*) = const. Но, так как при x=0 выражение (*) (точнее его левая часть) равно 0, то и const=0. Значит В – обратный оператор к (A - ![]() *I) в S.
*I) в S.
Итак, мы получили ограниченный оператор В, обратный к (A - ![]() *I), который существует при
*I), который существует при ![]()
![]()
![]() R, за исключением
R, за исключением ![]() =0, то есть все возможные
=0, то есть все возможные ![]()
![]() 0 – это регулярные точки оператора А; Сам же оператор В – резольвента оператора А. Спектр оператора А – значение
0 – это регулярные точки оператора А; Сам же оператор В – резольвента оператора А. Спектр оператора А – значение ![]() при которых В не существует, то есть
при которых В не существует, то есть ![]() =0.
=0.
Вывод:
Оператор интегрирования, действующий в пространстве непрерывных функций – C[a,b], определенных на отрезке [a,b], заданный следующим образом: Аf(t) = 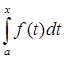 , где f(t) – функция, непрерывная на [a, b], t
, где f(t) – функция, непрерывная на [a, b], t ![]() [a,x]; x
[a,x]; x ![]() [a,b]; a,b
[a,b]; a,b![]() R:
R:
1. линейный;
2. непрерывный;
3. ограниченный: 0 ![]() |
|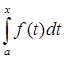 |
| ![]() |b-a|;
|b-a|;
4. норма A: ||A|| = (b-a);
5. резольвента оператора А: R![]() (A) = -
(A) = -![]() -
- ![]() *
*![]() *
* , где
, где
x ![]() [0,b], t
[0,b], t ![]() [0,x], g(x)
[0,x], g(x) ![]() S, S = {f
S, S = {f ![]() C[0,b] / f(0) = 0} с нормой ||f||=
C[0,b] / f(0) = 0} с нормой ||f||=![]() |f(x)|, g(x) =
|f(x)|, g(x) =  -
- ![]() *f(x),
*f(x), ![]() - произвольное число.
- произвольное число.
6. Спектр оператора А: ![]() =0.
=0.
§6. Оператор дифференцирования.
Рассмотрим оператор дифференцирования Д действующий в пространстве дифференцируемых функций – D[a,b], заданный следующим образом:
Дf(x) = f/(x);
Функция f(x) ![]() D[a, b], f/(x)
D[a, b], f/(x) ![]() C[a, b];
C[a, b];
Проверим оператор Д на линейность, по определению 1:
1) Аксиома аддитивности: Д(f+g) = Д(f) + Д(g).
Д(f+g) = (f+g)/ = f/ + g/ = Д(f) + Д(g).
2) Аксиома однородности: Д(kf) = kД(f).
Д(kf) = (kf) / = k(f)/ = kД(f).
Исходя из свойств производной:
1. производная от алгебраической суммы нескольких функций равна алгебраической сумме их производных;
2. постоянный множитель можно вынести за знак производной.
Можно утверждать, что Д – линейный оператор.
3) Для линейных операторов ограниченность и непрерывность оператора эквивалентны, это следует из теоремы 3.
3.1) Для начала покажем, что Д не является непрерывным оператором.
Задан оператор Дf(x) = f/(x) подпространства E ![]() C[0, 2
C[0, 2![]() ], состоящего из непрерывно дифференцируемых функций, в пространство C[0, 2
], состоящего из непрерывно дифференцируемых функций, в пространство C[0, 2![]() ].
].
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
