Преобразование и расчет характеристик математических моделей объекта управления

В свою очередь эти скорости определяются текущими значениями переменной состояния , управлениями и возмущениями , действующими на объект

>, (2.2)

где g = (g1, ., gn)T – вектор функция; x10 , x20. , xn0 – начальные условия.

Если g( ) – нелинейная функция, то решение уравнения (2.2) усложняется, так как сводится к интегрированию системы нелинейных ДУ. Так как методы интегрирования систем ДУ хорошо разработаны только для линейных систем, то перед работой с ними необходимо линеаризовать g( ) в окрестности рабочей точки, которой соответствует установившейся режим работы объекта.

Для линеаризованной функции g( ) ДУ вида (2.2) с учетом воздействия среды можно представить в векторной форме:

, (2.3)

где A(t); B(t); E(t) – матрицы преобразования, элементы которых в общем случае являются функциями времени.

Элементы xi в уравнении (2.3) называются переменными состояния объекта или фазовыми координатами. Переменные состояния (фазовые координаты) образуют вектор состояния, переменные управления и возмущения образуют векторы управления и возмущения. Множество этих векторов составляет пространство состояний (фазовое пространство) X, пространство управлений U и возмущений F.

Во многих физических объектах регулируются, измеряются и передаются по информационным каналам не значения вектора состояния , а другие значения – функции составляющих вектора фазовых координат, называемые управляемыми или выходными величинами. Обозначим измеряемые величины через y1(t), y2(t), ., ys(t), причем обычно s £ n. Тогда уравнение измерения, связывающее регулируемые, регулирующие и фазовые координаты объекта примет вид

. (2.4)

Для линейного объекта это соотношение линейное:

. (2.5)

Матрица С(t) называется матрицей измерения, матрица D(t) – форсирующая матрица. Ненулевая матрица D(t) свидетельствует о наличии в структуре объекта форсирующих звеньев. При измерениях, описываемых выражениями (2.4) и (2.5), вектором выходных сигналов (или просто вектором выхода) является вектор . Отметим, что между векторами входа, выхода и состояния существует принципиальное различие. Если все составляющие вектора входа и вектора выхода являются вполне конкретными физическими величинами, то элементами вектора состояния могут быть некоторые абстрактные переменные, физическая природа которых не всегда определена.

Векторно-матричная запись модели линейного динамического объекта с учетом уравнения измерения (2.5) принимает вид:

. (2.6)

Индексы матриц показывают их размерность. Если матрицы A(t), B(t), C(t) и D(t) не зависят от времени, то объект называется объектом с постоянными коэффициентами, или стационарным, объектом. В противном случае объект будет нестационарным.

При наличии погрешностей при измерении, выходные (регулируемые) сигналы задаются линеаризованным матричным уравнением:

, (2.7)

где – вектор регулируемых (измеряемых) величин; C(t) – матрица связи вектора измерений с вектором состояний; v(t) – вектор ошибок измерений (помехи).

Структура линейной непрерывной системы, реализующая уравнения (2.6) и (2.7) приведена на рис. 2.2.

Рис. 2.2.

Данная структура соответствует математической модели объекта построенной в пространстве состояний его входных u(t), выходных y(t) и внутренних, или фазовых координат x(t).

Пример 2. Рассмотрим математическую модель двигателя постоянного тока с независимым возбуждением от постоянных магнитов.

Система уравнений электрической и механической частей двигателя для рассматриваемого случая будет выглядеть:

. (2.8)

Первое уравнение отражает взаимосвязь между переменными в цепи якоря, второе - условия механического равновесия. В качестве обобщенных координат выберем тока якоря I и частоту вращения якоря w. Управлением являются напряжение на якоре U, возмущением момент сопротивления нагрузки Mc. Параметрами модели являются активное сопротивление и индуктивность цепи и якоря, обозначенные соответственно Rя, и Lя, а также приведенный момент инерции J и конструктивные постоянные се и см. В системе СИ се = см.

Разрешая исходную систему относительно первых производных, получим уравнения двигателя в пространстве состояний.

. (2.9)

В матричном виде уравнения (2.9) примут вид (2.6)

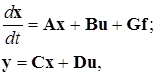(2.10)

где вектор обобщенных координат , вектор управлений (в рассматриваемом случае он является скаляром), вектор (скаляр) возмущений . Матрицы модели

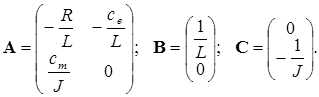(2.10)

Если в качестве регулируемой величины выбрать частоту вращения, то уравнение измерения запишется в виде , а матрицы CиD примут вид

.

3. Дискретные структурированные модели

Структурная схема, приведенная на рис. 3.1, содержит как дискретные, таки непрерывные элементы, соединенные между собой благодаря наличию АЦП и ЦАП. Однако провести расчет такой системы с помощью математического аппарата непрерывных линейных систем управления, рассмотренного в предыдущих разделах, невозможно из-за наличия дискретных элементов.

Рис. 3.1 Структурная схема СУ с учетом запаздывания в ЭВМ.

Для математического описания дискретных систем, по аналогии с непрерывными системами введем понятие решетчатой функции, являющейся аналогом непрерывной функции.

 Скачать реферат