Преобразование и расчет характеристик математических моделей объекта управления

. (1.6)

Преобразовывая по Лапласу (1.6) и группируя подобные члены, получим выражение аналогичное (1.4).

, (1.7)

где - единична

я матрица.

Полагая , а найдем взаимосвязь параметров структурированной модели и модели в пространстве состояний

, , . (1.8)

По аналогии с одномерными системами, используя основные правила теории матриц, можно ввести понятие матрицы передаточной функции.

Если умножить (1.4) на обратную матрицу , то получим:

(1.9)

Отсюда можно получить выражение для матриц передаточных функций системы по управлению

(1.10)

и возмущению

(1.11)

Как для одномерных, так и для многомерных систем одной и той же матрице передаточной функции может соответствовать несколько вариантов структурных схем и уравнений состояния.

Т.е. по уравнениям состояния матрица передаточной функции может быть получена однозначно, обратное утверждение будет неверным. Это связано с тем, что при получении выражения передаточной функции исключаются из рассмотрения все внутренние переменные структурированной модели, которые нельзя уже восстановить по выражению передаточной функции.

Пример 1.Пусть имеется передаточная функция звена, записанная в виде:

. (1.12)

Запишем ее через отрицательные степени оператора р.

. (1.13)

Введем вспомогательную переменную Е(р) равную

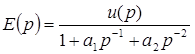, (1.14)

Или , (1.15)

откуда нетрудно составить и структурную схему (рис. 1.1).

Рис. 1.1

Дифференциальные уравнения для переменных состояния могут быть легко найдены из рассмотрения структурной схемы системы.

. (1.16)

Разложим (1.12) на простейшие дроби, предполагая, что характеристическое уравнение звена имеет действительные корни p1 и p2 . Согласно теореме Виетта

, .

Тогда выражение передаточной функции примет следующий вид:

, (1.17)

где ,.

Структурная схема следует из выражения передаточной функции непосредственно (рис. 1.2).

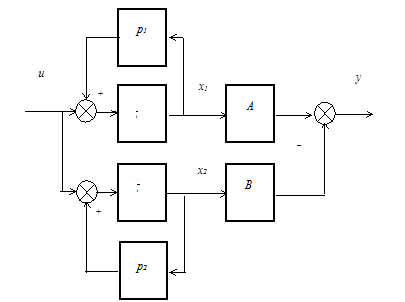
Рис. 1.2

Система дифференциальных уравнений теперь выглядит

. (1.18)

Если теперь записать (1.12) в виде произведения дробей, то получим следующее выражение

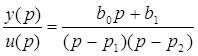(1.19)

Введем переменные состояния

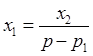
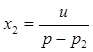, тогда

.

Отсюда можно получить структурную схему (рис. 1.3) и уравнения в переменных состояния

(1.20)

Рис. 1.3.

Сравнивая уравнения состояния (1.16), (1.18) и (1.20) и структурные схемы рис. 1.1 – 1.3, можно сделать вывод о том, что одной передаточной функции (1.12) могут соответствовать различные структуры и уравнения состояния. Такое многообразие структурных схем обусловлено выбором различных систем отсчета (базисов) для переменных состояния. Выбирая переменные состояния в различных координатных системах (базисах) можно получать и различные структурные схемы.

2. Непрерывные модели пространства состояния

Математическая модель (образ) представляет собой абстрактное отражение реального объекта (оригинала, прообраза). В зависимости от типа объекта и целей, ради которых строится и используется модель, формальное описание может быть различным. Для моделирования объектов могут быть использованы структурные схемы, операторные уравнения, алгебраические уравнения, дифференциальные, интегральные и интегро-дифференциальные уравнения, Марковские цепи, передаточные функции, частотные характеристики, весовые функции, графы и т. д. Все эти методы функционально связывают входные и выходные сигналы объекта. По количеству входов и выходов объекты и соответствующие им модели разделяют на одномерные и многомерные. Одномерными называют объекты, имеющие один вход и один выход, многомерными – объекты, имеющие несколько входов и выходов, причем число входов не обязательно равно числу выходов. Блок-схемы одномерного и многомерного объектов изображены соответственно на рис. 2.1,а и рис. 2.1,б. Причем число входов не обязательно равно числу выходов.

Рис. 2.1.

Наиболее полно объект описывается в терминах пространства состояний. Под состоянием объекта понимается совокупность величин xi, полностью определяющих его положение в данный момент времени.

Наиболее употребительной моделью динамических объектов являются дифференциальные уравнения. Будем рассматривать только объекты с сосредоточенными параметрами, которые описываются обыкновенными дифференциальными уравнениями. Порядок системы дифференциальных уравнений, описывающей модель объекта, непосредственно не определяется количеством входов и выходов, а зависит от операторов, преобразующих входные сигналы в выходные.

Для динамических систем, в которых физические процессы протекают непрерывно во времени, скорости изменения переменной состояния объекта можно также задать вектором

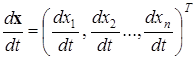, (2.1)

где , – скорости изменения компонент многомерной переменной состояния.

 Скачать реферат