Преобразование и расчет характеристик математических моделей объекта управления

Решетчатая функция это импульсная функция, состоящая из периодически следующих друг за другом δ – импульсов, площадь которых равна значениям непрерывного сигнала в те же моменты времени.

Графически преобразование непрерывного сигнала в импульсный сигнал с помощью решетчатой функции можно изобразить таки образом

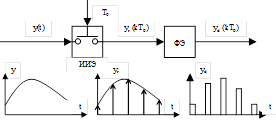
Рис. 3.2. Формирование импульсного сигнала с помощью решетчатой функции.

На схеме рис. 3.2 АЦП заменен идеальным импульсным элементом (ИИЭ) и формирующим элементом (ФЭ). Идеальный импульсный элемент формирует на выходе δ – импульсы, площадь которых модулирована уровнем входного сигнала, т.е. идеальный импульсный элемент формирует на своем выходе решетчатую функцию от входного сигнала.

, k=0, 1, 2,… (3.1)

Формирующий элемент является непрерывным с функцией веса равной выходному сигналу ФЭ. Это следует из определения функции веса, которая есть реакция элемента на δ – импульс. Именно такие импульсы и действуют на входе ФЭ. Зная функцию веса нетрудно вычислить и передаточную функцию ФЭ.

. (3.2)

Передаточная функция ФЭ вычисляется от одиночного импульса yd .

Введение понятия идеального импульсного элемента и решетчатой функции является математической абстракцией, позволяющей установить аналитическую связь между непрерывным и импульсным сигналом [83].

Вычислим передаточную функцию ФЭ – который генерирует на выходе прямоугольные импульсы с амплитудой А и длительностью tи.

. (3.3)

Если теперь в (3.3) положить , то мы получим передаточную функцию экстраполятора нулевого порядка, поскольку на интервале времени в отсутствии импульсов на выходе ФЭ на его выходе сигнал будет сохранять постоянное значение равное площади входного δ – импульса.

Найдем теперь выражение для дискретной передаточной функции дискретного элемента, у которого входной и выходной сигналы соответственно равны

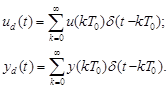(3.4)

Вычислим y(t) используя теорему о свертке или интеграл Дюамеля.

В дискретной форме этот интеграл заменится бесконечной суммой

. (3.5)

Если квантование входного и выходного сигналов осуществляется синхронно, то выходное время и (3.5) запишется так

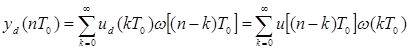. (3.6)

Найдем теперь дискретное изображение по Лапласу от y(t). Для этого в преобразовании Лапласа также заменим интеграл суммой

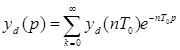. (3.7)

Подставим в (3.7) (3.6) получим

. (3.8)

Сделаем замену m=n-k и изменим очередность суммирования членов

(3.9)

В (3.9) первая сумма есть ничто иное, как дискретное преобразование Лапласа от функции веса, или дискретная передаточная функция, второе слагаемое представляет собой дискретное преобразование Лапласа от входного сигнала. Следовательно, можно записать

. (3.10)

Откуда (3.11)

Дискретная передаточная функция есть отношение дискретных изображений по Лапласу выходной к входной величине при нулевых начальных условиях.

В теории дискретных систем более широко применяется z- преобразование, введенное в рассмотрение Джури. По сути дела z- преобразование есть модифицированное преобразование Лапласа, получаемое путем замены оператора

. (3.12)

Тогда дискретная передаточная функция по переменной z запишется в виде

. (3.13)

Дискретная передаточная функция по переменной z есть отношение z –преобразований выходной величины к входной при нулевых начальных условиях.

4. Дискретные модели пространства состояния

.В том случае если объект управления многомерный и имеет математическую модель, заданную в пространстве состояний, то последняя сводится к дискретной модели вида

, (4.1)

где параметры (матрицы) дискретной системы связаны с параметрами (матрицами) исходной непрерывной выражениями [78]

(4.2)

где Т0 – интервал квантования.

Докажем это утверждение. Известно [36, 65], что решение матричного дифференциального уравнения,

, (4.3)

заданного в пространстве состояний при начальных условиях x(0) описывается выражением

, (4.4)

Матрица Ф(t)

, (4.5)

которую определяют как переходную, определяется как ряд

. (4.6)

Дискретная форма записи решения (3.45) при условии, что входной сигнал остается постоянным во время такта квантования, запишется так

. (4.7)

Вводя новую переменную и подставляя ее в (4.7) получим

. (4.8)

Откуда с учетом (4.5) непосредственно следует (4.2)

Пример 4.1. Найдем дискретную модель в пространстве состояний исполнительного механизма, уравнения состояния которого имеют вид:

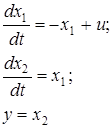. (4.9)

Для вычисления матричной экспоненты (4.5) найдем ее преобразование Лапласа, которое будет равно.

(4.10)

I – единичная матрица.

После подстановки в него матрицы А получим

. (4.11)

Вычислим обратную матрицу

. (4.12)

Откуда, осуществляя z – преобразование последней матрицы, найдем матрицу перехода дискретной системы Ad

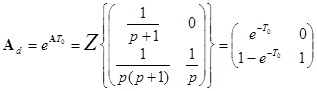. (4.13)

где Т0 – интервал дискретизации по времени.

Матрица Bd будет равна

. (4.14)

Тогда дискретный аналог модели исполнительного механизма будет выглядеть

 Скачать реферат