Преобразование и расчет характеристик математических моделей объекта управления

.

Переход в пространство состояний дискретной модели можно осуществить из структурированной непрерывной или дискретной модели, заданной соответствующей передаточной функцией.

В первом случае, когда имеется передаточная функция непрерывной модели возможно

два варианта перехода. В первом варианте получают непрерывную модель в пространстве состояний, как это рассмотрено в примере 1, а затем по выражениям (4.2) получают дискретную модель. Во втором варианте перехода сначала из непрерывной передаточной функции получают дискретную передаточную функцию. Полученную дискретную передаточную функцию разлагают на простые дроби по переменной z, а затем для каждой полученной простой дроби находят ее АРСС – модель первого порядка. Система таких АРСС – моделей для каждой простейшей дроби и образует дискретную модель в пространстве состояний.

Пример 4.2 Перейдем от дискретной передаточной функции вида

(4.15)

к дискретной модели в пространстве состояний.

Введем вспомогательную переменную x1(z) и запишем (4.14) в виде

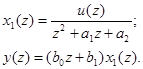(4.16)

По уравнениям (4.16) получим АРСС- модель

(4.17)

Введем еще одну переменную

. (4.18)

Подставляя ее в (4.17) получим дискретную модель в пространстве состояний

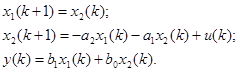(4.19)

как в примере 1 можно использовать другие формы разложения передаточной функции (4.15), получая соответственно и другие виды эквивалентных ей уравнений состояния дискретной системы.

Для дискретной системы также справедливы линейные преобразования в пространстве состояний задаваемые с помощью матрицы перехода.

. (4.20)

5. Расчет

5.1. Расчёт параметров МПС

Придется исходную функцию привести в виде произведения 2-х передаточных функций

где

Запишем дифференциальные уравнения звеньев системы:

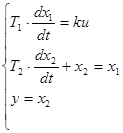
Полученную систему приведём к нормальному виду:

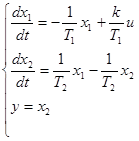
По полученному уравнению найдём параметры матрицы системы:

, , , .

, , ,

5.2 Расчёт параметров модели дискретной передаточной функции

Разложим исходную передаточную функцию на дроби:

Вычислим от

, - период дискретизации

Зная дискретную передаточную функцию апериодического звена найдём передаточную функцию исходной системы:

,

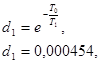
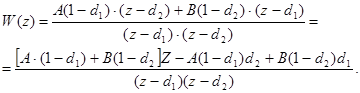
Приведём к нормальному виду:

,

,

,

,

,

-0.7192,

0,00003615,

2.4783,

0.2615.

5.3 Расчёт параметров дискретной МПС модели

Для расчетов параметров МПС воспользуемся дискретной передаточной функцией, записав её в следующем виде:

,

,

.

Дискретная модель так же состоит из 2-х простых моделей представленном на рисунке 5.1

Рисунок 5.1

,

.

Запишем разности уравнения полученной модели

,

.

От уравнения записанного в символьной форме переходим к реальному разностному уравнению. Запишем:

,

,

,

,

,

.

В последнем уравнении заменим его выражением:

 Скачать реферат