Модели поведения производителей

(42)

Значит, равновесные объемы выпуска q1* и q2* обеспечивают максимум прибыли как для лидера, так ж дня последователя при принятых, условиях их стратегического взаимодействия.

Решение модели Стэкльберга можно найти, используя другой алгоритм.

Поставив функцию зависимости q2 от q1 из уравнения (35) в функцию прибыли фирмы-лидера (7), получим:

(43)

Таким образом, лидер решает задачу максимизации прибыли на безусловный экстремум, где в процессе принятия решений он осознает, что отраслевой выпуск составит q1+q2(q1), т.е. учитывает реакцию последователя.

Необходимое условие экстремума:

(44)

позволяет однозначно определить наилучшее решение фирмы-лидера (достаточное условие экстремума 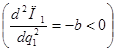подтверждает принятие наилучшего решения). Подставив найденный уровень выпуска первой фирмы в уравнение реакции (35) фирмы-последователя, получим равновесный уровень выпуска второй фирмы. Учитывая, что линия реакции представляет наилучший ответ на действия конкурента, равновесный уровень выпуска фирмы-последователя обеспечит ей максимум прибыли при заданных условиях взаимодействия.

Равновесные уровни выпуска дуополистов Стэкльберга обеспечивают удовлетворение рыночного спроса в объеме

(45)

при равновесной цене

(46)

При этом в соответствии с предпосылками рассматриваемой модели лидер получает прибыль в размере

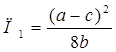(47)

что в два раза превышает уровень прибыли последователя.

2.4 Картельное соглашение

Один из примеров кооперированной олигополии - сговор между фирмами-конкурентами. Картель - это объединение олигополистов, вступающих в сговор с целью совместного принятия решения относительно уровня рыночной цены и объемов выпускаемой продукции. Образующие картель фирмы ведут себя на рынке как единый монополист, максимизируя совокупную прибыль отрасли.

Рассмотрим картель, максимизирующий прибыль при предпосылках (1)- (3). Задача максимизации прибыли для двух фирм заключается в выборе таких уровней выпуска продукции q1 и q2, которые бы максимизировали совокупную прибыль отрасли П, где

(48)

Необходимое условие экстремума имеет вид:

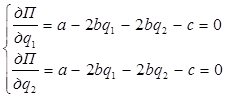(49)

Оно определяет систему двух одинаковых уравнений с двумя неизвестными (q1 и q2), которая имеет бесконечно много решений. Любая комбинация объемов выпуска фирм (q1,q2), которая обеспечивает рыночный спрос в размере

(50)

Удовлетворяет системе уравнений (49).

Таким образом, необходимое условие экстремума задает лишь совокупный объем производства картеля. Достаточное условие экстремума с учетом вида функции (48) и знака вторых частных производных

(51)

указывает на то, что будет обеспечен максимально возможный уровень совокупной прибыли отрасли в размере

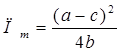(52)

при монопольной цене

(53)

Распределение рыночных долей с точки зрения максимизации совокупной прибыли отрасли значения не имеет. Однако существует проблема согласования решений между членами картеля. Поскольку в нашей модели фирмы идентичны по издержкам производства, логично предположить, что их рыночные доли будут одинаковыми, т.е.

(54)

При этом члены картеля получают одинаковую прибыль в размере

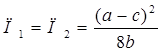(55)

В принципе переговоры относительно распределения рыночных долей могут быть проведены на множестве комбинаций объемов выпуска фирм. В случае максимизации совокупной прибыли отрасли предельная прибыль от производства дополнительной единицы продукции будет одинаковая (вне зависимости от того, кто из членов картеля произведет эту дополнительную единицу).

Основная проблема любого картельного соглашения - соблазн обмануть конкурента, т.е. нарушить соглашение и увеличить собственную прибыль.

Пусть в нашей модели вторая фирма честно соблюдает соглашение, в то время как первая фирма решила его нарушить. Для аналитической версии модели это означает, что первая фирма будет максимизировать свою прибыль (7) при нулевой предполагаемой вариации и фактически будет выбирать уровень своего выпуска в соответствии с линией реакции Курно (12).

Ориентируясь на уровень выпуска конкурента (54), соответствующий заключенному картельному соглашению, первая фирма выберет на линии реакции точку N, увеличив уровень своего выпуска до

 Скачать реферат