Модели поведения производителей

где а, b - положительные константы; рыночный спрос Q складывается из объемов предложения первой и второй фирм (Q = q1 + q2 ) при цене Р.

Пусть также обе фирмы имеют равные условия по издержкам производства:

(2) ТCi = сqi

где с - положительная константа.

Таким образом, предельные издержки равны средним для каждого дуополиста:

(3) MCi=ACi=c

2.1 Модель Курно

Модель Курно - одна из классических моделей количественной олигополии. Аналитическая версия модели анализирует стратегическое взаимодействие фирм при нулевых предполагаемых вариациях:

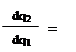(4) 0; 0

Это означает, что при решении задачи на максимум прибыли каждый дуополист рассматривает уровень выпуска конкурента как постоянный, и при данной предпосылке принимает решение об уровне своего выпуска.

Прибыли дуополистов определяются как разности между выручкой и издержками каждого из них:

(5) П1=TR1-TC1;

(6) П2=TR2-TC2

При предпосылке, что им известна функция рыночного спроса (1), получим-

(7)

(8) П2=(a-bq1-bq2)q2-cq2

Необходимое условие максимизации прибылей дуополистов:

(9)

Примет вид:

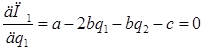(10)

(11)

Уравнения (10) и (11) задают линии реакции дуополистов и могут быть переписаны в виде:

(12)

(13)

Равновесие на рынке дуополии Курно определяется в результате решения (решение имеет смысл лишь при а>с) системы уравнений (12), (13):

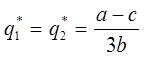(14)

Достаточное условие максимизации прибылей дуополистов показывает, что частные производные второго порядка функций прибыли отрицательны:

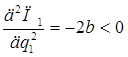(15)

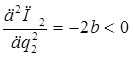(16)

Значит, равновесные объемы выпуска q1* и q2* обеспечивают максимум прибыли для каждого дуополиста.

Равновесные уровни выпуска дуополистов Курно одинаковы в силу введенных предпосылок об однородности продукции и о равновесных условиях по издержкам производства. Они обеспечивают удовлетворение рыночного спроса в объеме

(17)

при равновесной цене

(18)

что позволяет каждому дуополисту получить прибыль в размере

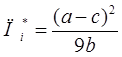(19)

2.2 Модель Чемберлина

Аналитическая версия модели Э. Чемберлина основана на экономическом анализе рынка олигополии, сделанном в его монографии, опубликованной в 1956 г. В отличие от модели Курно в модели Чемберлина дуополист принимает во внимание тот факт, что уровень конкурента будет изменяться в ответ на его собственные действия. В результате дуополисты примут наиболее выгодные для себя решения, не вступая в открытый сговор.

Рассмотрим возможный алгоритм стратегических взаимодействий в дуополии Чемберлина. Предположим, что на первом шаге, для примера, первая фирма ведет себя на рынке как монополист. Решая задачу на максимум прибыли, она выбирает монопольный уровень выпуска:

(20)

При этом она получит монопольную прибыль

(21)

при монопольной цене

(22)

На втором шаге вторая фирма принимает решение исходя из функции остаточного спроса на свою продукцию и предполагая, что выпуск первой фирмы не изменится. Таким образом, вторая фирма фактически принимает решение как фирма-монополист, где уравнение функции остаточного спроса имеет вид:

(23)

Решая задачу на максимум прибыли, она выбирает уровень выпуска

(24)

что составляет половину монопольного выпуска первой фирмы. В результате отраслевой выпуск составит

 Скачать реферат