Многомерный статистический анализ в системе SPSS

Рис. 4.2.2. Лямбда Уилкса

По коэффициенту Уилкса (рис. 4.2.2) для второй функции значимость более 0.001, следовательно, ее для дискриминации использовать нецелесообразно.

Данные таблицы «Результаты классификации» (рис. 4.2.3) свидетельствуют о том, что для 93,3 % наблюдений классификация проведена корректно, высокая точность достигнута в первой и второй группах (100% и 91,7%), менее т

очные результаты получены в третьей группе (88, 9%).

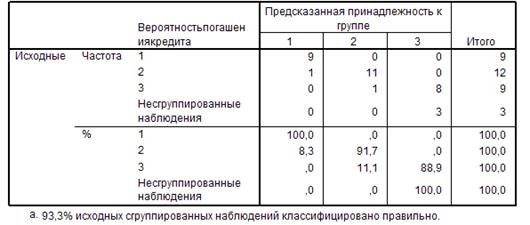
Рис. 4.2.3. Результаты классификации

Информация о фактических и предсказанных группах для каждого клиента приведены в таблице «Поточечные статистики» (рис. 4.2.4).

В результате дискриминантного анализе высокой вероятностью определена принадлежность новых клиентов банка к обучающему подмножеству М3 – первый, второй и третий клиент (порядковый номера 31, 32, 33) отнесены к подмножеству М3 с соответствующими вероятностями 99%, 99% и 100%.

Рис. 4.2.4. Поточечная статистика

Рис. 4.2.5. Функции в центроидах групп

Координаты центроидов по группам приведены в таблице «Функции в центроидах групп» (рис. 4.2.5). Они используются для нанесения центроидов на карту восприятия (рис. 4.2.6).

Поле «Территориальной карты» разделено дискриминантными функциями на три области: в левой части находятся преимущественно наблюдения первой группы клиентов с очень низкой вероятностью погашения кредита, в правой части — третьей группы с высокой вероятностью, в средней — второй группы клиентов со средней вероятностью возврата кредита соответственно.

На рис. 4.2.7 (а – в) отражено расположение клиентов каждой из трех групп на плоскости двух дискриминантных функций D1(X) и D2(X). По этим графикам можно проводить детальный анализ вероятности погашения кредита внутри каждой группы, судить о характере распределения клиентов и оценивать степень их удаленности от соответствующего центроида.

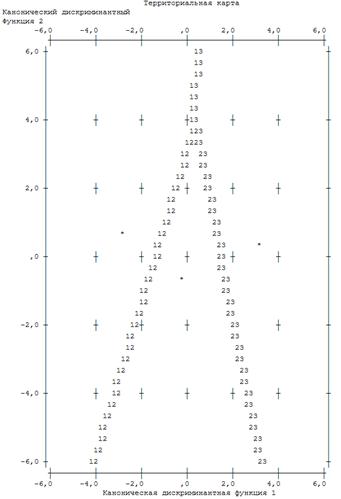
Рис. 4.2.6. Карта восприятия для трех дискриминантных функций D1(X) и D2(X) (* — центроид группы)

Так же на рис. 4.2.7 (г) в той же системе координат приведен объединенный график распределения всех групп клиентов вместе со своими центроидами; его можно использовать для проведения сравнительного визуального анализа характера взаимного расположения групп клиентов банка с разными вероятностями погашения кредита. В левой части графика расположены заемщики с высокой вероятностью погашения кредита, в правой — с низкой, а в средней части — со средней вероятностью. Поскольку по результатам расчета вторая дискриминантная функция D2(X) оказалась незначима, то различия координат центроидов по этой оси незначительны.

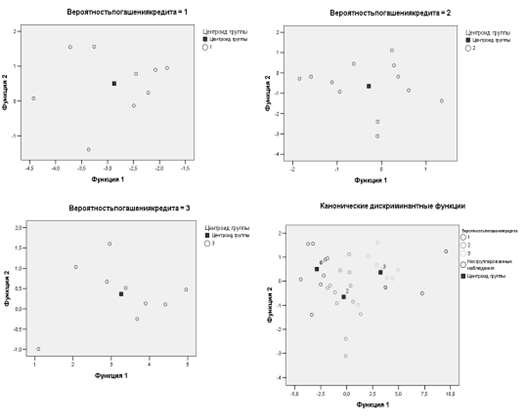
Рис. 4.2.7. Расположение наблюдений на плоскости двух дискриминантных функций для групп с низкой (а), средней (б), высокой (с) вероятностью погашения кредита и для всех групп (г)

Список литературы

1. «Многомерный статистический анализ в экономических задачах. Компьютерное моделирование в SPSS», Вузовский учебник, 2009 г.

 Скачать реферат