Многомерный статистический анализ в системе SPSS

Требуется:

На основе дискриминантного анализа с использованием пакета SPSS определить, к какой из четырех категорий относятся три заемщика (юридических лица), желающие получить кредит в коммерческом банке:

§ Группа 1 — с отличными финансовыми показателями;

§ Группа 2 — с хорошими финансовыми показателями;

§ Группа 3 — с плохими финансовыми показателями;

§ Группа 4 — с очен

ь плохими финансовыми показателями.

По результатам расчета построить дискриминантные функции; оценить их значимость по коэффициенту Уилкса (λ). Построить карту восприятия и диаграммы взаимного расположения наблюдений в пространстве трех функций. Выполнить интерпретацию результатов проведенного анализа.

Ход выполнения:

Для того чтобы определить, к какой из четырех категорий относятся три заемщика, желающие получить кредит в коммерческом банке, строим дискриминантный анализ, который позволяет определить, к какой из ранее выявленных совокупностей (обучающих выборок) следует отнести новых клиентов.

В качестве зависимой переменной выберем группу, к которой может относиться заемщик в зависимости от его финансовых показателей. Из данных задачи, каждой группе присваивается соответствующая оценка 1, 2, 3 и 4.

Ненормированные канонические коэффициенты дискриминантных функций, приведенные на рис. 4.1.1, используются для построения уравнения дискриминантных функций D1(X), D2(X) и D3(X):

1.) D1(X) =

2.) D2(X) =

3.) D3(X) =

Рис. 4.1.1. Коэффициенты канонической дискриминантной функции

Рис. 4.1.2. Лямбда Уилкса

Однако, поскольку значимость по коэффициенту Уилкса (рис. 4.1.2) второй и третей функции более 0.001, их для дискриминации использовать нецелесообразно.

Данные таблицы «Результаты классификации» (рис. 4.1.3) свидетельствуют о том, что для 100 % наблюдений классификация проведена корректно, высокая точность достигнута во всех четырех группах (100 %).

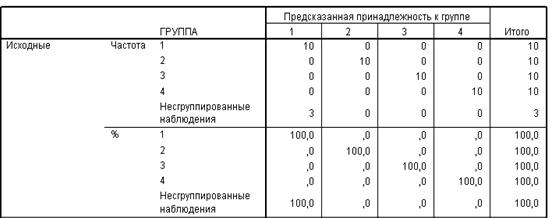
Рис. 4.1.3. Результаты классификации

Информация о фактических и предсказанных группах для каждого заемщика приведены в таблице «Поточечные статистики» (рис. 4.1.4).

В результате дискриминантного анализе высокой вероятностью определена принадлежность новых заемщиков банка к обучающему подмножеству М1 – первый, второй и третий заемщик (порядковый номера 41, 42, 43) отнесены к подмножеству М1 с соответствующими вероятностями 100 %.

 Скачать реферат