Многомерный статистический анализ в системе SPSS

Рис. 4.1.4. Поточечная статистика

Координаты центроидов по группам приведены в таблице «Функции в центроидах групп» (рис. 4.1.5). Они используются для нанесения центроидов на карту восприятия (рис. 4.1.6).

Рис. 4.1.5. Функции в центроидах групп

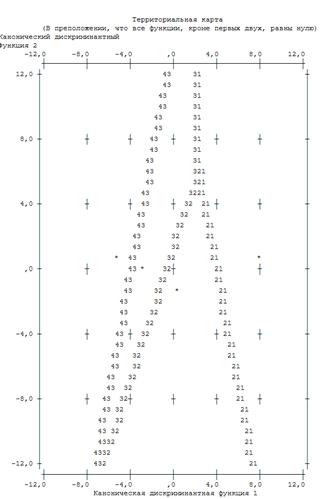
Рис. 4.1.6. Карта восприятия для двух дискриминантных функций D1(X) и D2(X) (* — центроид группы)

Поле «Территориальной карты» разделено дискриминантными функциями на четыре области: в левой части находятся преимущественно наблюдения четвертой группы заемщиков с очень плохими финансовыми показателями, в правой части — первой группы с отличными финансовыми показателями, в средней и нижней части — третьей и второй группы заемщиков с плохими и хорошими финансовыми показателями соответственно.

Рис. 4.1.7. Диаграмма рассеяния для всех групп

На рис. 4.1.7 приведен объединенный график распределения всех групп заемщиков вместе со своими центроидами; его можно использовать для проведения сравнительного визуального анализа характера взаимного расположения групп заемщиков банка по финансовыми показателями. В правой части графика расположены заемщики с высокими показателями, в левой — с низкой, а в средней части — со средними финансовыми показателями. Поскольку по результатам расчета вторая дискриминантная функция D2(X) оказалась незначима, то различия координат центроидов по этой оси незначительны.

Оценка кредитоспособности физических лиц в коммерческом банке

Кредитный отдел коммерческого банка провел выборочное обследование 30 своих клиентов (физических лиц). На основе предварительного анализа данных, заемщики оценивались по шести показателям (табл. 4.2.1):

Х1 — заемщик брал кредит в коммерческих банках ранее;

Х2 — среднемесячный доход семьи заемщика, тыс. руб.;

Х3 — срок (период) погашения кредита, лет;

Х4 — размер выданного кредита, тыс. руб.;

Х5 — состав семьи заемщика, чел.;

Х6 — возраст заемщика, лет.

При этом по вероятности возврата кредита выявлены три группы заемщиков:

§ Группа 1 — с низкой вероятностью погашения кредита;

§ Группа 2 — со средней вероятностью погашения кредита;

§ Группа 3 — с высокой вероятностью погашения кредита.

Требуется:

На основе дискриминантного анализа с использованием пакета SPSS необходимо классифицировать трех клиентов банка (по вероятности погашения кредита), т.е. оценить принадлежность каждого из них к одной из трех групп. По результатам расчета построить значимые дискриминантных функции, их значимость оценить по коэффициенту Уилкса (λ). В пространстве двух дискриминантных функций для каждой группы построить диаграммы взаимного расположения наблюдений и объединенную диаграмму. Оценить место расположения каждого заемщика на этих диаграммах. Выполнить интерпретацию результатов проведенного анализа.

Таблица 4.2.1. Исходные данные

Ход выполнения:

Для построения дискриминантного анализа в качестве зависимой переменной выберем вероятность своевременного погашения кредита клиентом. Учитывая, что она может быть низкой, средней и высокой, каждой категории присвоим соответствующую оценку 1,2 и 3.

Ненормированные канонические коэффициенты дискриминантных функций, приведенные на рис. 4.2.1, используются для построения уравнения дискриминантных функций D1(X), D2(X):

1.) D1(X) =

2.) D2(X) =

Рис. 4.2.1. Коэффициенты канонической дискриминантной функции

 Скачать реферат