Математические методы в решении экономических задач
Приступаем к решению задачи.
Требуется составить план производства изделий А₁ и А₂ обеспечивающий максимальную прибыль предприятия от реализации готовой продукции. Необходимо:
Решить задачу геометрически;
Решить задачу симплекс-методом(аналитическим и табличным)
Сформулировать двойственную задачу и найти её решение.
Задача №1
Предприятие предполагает выпускат
ь два вида продукции А₁ и А₂, для производства которых используется сырьё трех видов. Производство обеспечено сырьем каждого вида в количествах: b₁, b₂, b₃ кг. На изготовление единицы изделия А₁ требуется затратить сырья каждого вида а₁₁, а₂₁, а₃₁ кг, соответственно, а для единицы изделия А₂ - а₁₂, а₂₂, а₃₂ кг. Прибыль от реализации единицы изделия А₁ составляет с₁ ден.ед., для единицы изделия А₂ - с₂ ден.ед.
Вспомогательная таблица
|
Вид сырья |
Продукция |
Ограничения по сырью | |
|
А₁ |
А₂ | ||
|
1-й |
а₁₁ |
а₁₂ |
b₁ |
|
2-й |
а₂₁ |
а₂₂ |
b₂ |
|
3-й |
а₃₁ |
а₃₂ |
b₃ |
|
прибыль |
с₁ |
с₂ | |
Решение задачи геометрическим методом
Трудность построения математической модели заключается в идентификации переменных и последующем представлении цели и ограничений в виде математических функций этих переменных. Если модель содержит только две переменные, то задачу линейного программирования можно решить графически. В случае трёх переменных графическое решение становится менее наглядным, а при большем значении переменных – даже невозможным. Однако графическое решение позволяет сделать выводы, которые служат основой для разработки общего метода решения задачи линейного программирования.
Первый шаг при использовании графического метода заключается в геометрическом представлении допустимых решений, т.е. построении области допустимых решений (ОДР.), в которой одновременно удовлетворяются все ограничения модели. При получении графического решения переменная X1 откладывается по горизонтальной оси, а X2 – по вертикальной. При формировании ОДР необходимо предотвратить получение недопустимых решений, которые связаны с необходимостью выполнения условия неотрицательности переменных. Перед построением необходимо определить квадранты, в которых будет располагаться ОДР. Квадранты определяются знаками переменных X1 и X2. Условия неотрицательности переменных X1 и X2 ограничивают область их допустимых значений первым квадрантом. Если переменная X1 не ограниченна в знаке, то область ограничивается первым и вторым квадрантом, если X2, то – первым и четвёртым квадрантом.
Области, в которых выполняются соответствующие ограничения в виде неравенств, указываются стрелками, направленными в сторону допустимых значений переменных.
В результате построений получается многоугольник, который определяет пространство решений. Если одно из ограничений имеет знак "=", то ОДР вырождается в отрезок.
В каждой точке, принадлежащей области или границам многоугольника решений, все ограничения выполняются, поэтому все решения, соответствующие этим точкам, являются допустимыми. Пространство решений содержит бесконечное число таких точек, несмотря на это, можно найти оптимальное решение. Для этого необходимо построить в плоскости переменных X1, X2 градиент целевой функции. Определение оптимальной точки зависит от той задачи, которую необходимо решить.
Если в целевой функции определена задача максимизации, то оптимальная точка будет располагаться в направлении увеличения градиента, если задача минимизации – то в направлении уменьшения градиента целевой функции. Для определения оптимальной точки будем перемещать целевую функцию в направлении увеличения (уменьшения) градиента до тех пор, пока она не сместиться в область недопустимых решений.
После нахождения оптимальной точки пространства решений определяют её координаты X1 *, X2 *и значение целевой функции F * в ней. Правильность выбора оптимальной точки можно проверить расчётом целевой функции в вершинах многогранника решений. В ЗЛП область допустимых решений всегда является выпуклым множеством, т.е. таким множеством, что наряду с любыми двумя точками, принадлежащими этому множеству, этому же множеству принадлежит и отрезок, соединяющий эти две точки. Любая функция наискорейшим образом увеличивается в направлении своего градиента.
Далее приступаем к решению задачи:
Занесём необходимые нам данные во вспомогательную таблицу:
|
Вид сырья |
Продукция |
Ограничения по сырью | |
|
А₁ |
А₂ | ||
|
1-й |
5 |
2 |
750 |
|
2-й |
4 |
5 |
807 |
|
3-й |
1 |
7 |
840 |
|
прибыль |
30 |
49 | |
Решение:
Предположим, что будет изготовлено Х₁ единиц изделий вида А₁ и Х₂ единиц - вида А₂. Поскольку производство продукции ограничено имеющимися в распоряжении предприятия сырьем каждого вида и количество изготовляемых изделий не может быть отрицательным, должны выполняться неравенства:
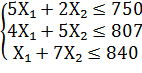
![]()
Другие рефераты на тему «Экономико-математическое моделирование»:
Поиск рефератов
Последние рефераты раздела
- Выборочные исследования в эконометрике
- Временные характеристики и функция времени. Графическое представление частотных характеристик
- Автоматизированный априорный анализ статистической совокупности в среде MS Excel
- Биматричные игры. Поиск равновесных ситуаций
- Анализ рядов распределения
- Анализ состояния финансовых рынков на основе методов нелинейной динамики
- Безработица - основные определения и измерение. Потоки, запасы, утечки, инъекции в модели
