Математические методы в решении экономических задач

Исходные данные транспортной задачи обычно записываются в таблице:

Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения. Проверяем выполнение необходимого и достаточного условия разрешимости задачи. Находим суммарные запасы поставщиков и запросы потребителей: 400 + 370 + 380 = 1150, 250 + 200 + 290 + 260 + 150 = 1150. => задача с правильным балансом. Составляем начальное опорное решение:

Таблица (1;1)

Т.к. n + m – 1 = 3 + 5 – 1 = 7, а в нашей задаче заполненных клеток всего 6, введём дополнительное число - нуль, на пересечении U1 и V2.

Получаем решение:

X1 = 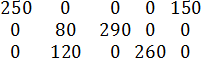- опорное решение №1.

Вычисляем значение целевой функции на этом опорном решении F = 250·2+ 150·3 + 80·8 + 290·6 + 120·15 + 260·9 = 500 + 450 + 640 + 1740 + 1800 + 2340 = 7470.

Для проверки оптимальности опорного решения необходимо найти потенциалы и оценки. По признаку оптимальности в каждой занятой опорным решением клетке таблицы транспортной задачи сумма потенциалов равна стоимости

Ui + Vj = Сij

Записываем систему уравнений для нахождения потенциалов:

U1 + V1 = 2,

U1 + V2 = 4,

U1 + V5 = 3,

U2 + V2 = 8,

U2 + V3 = 6,

U3 + V2 = 15,

U3 + V4 = 9

Далее одному из потенциалов задаем значение произвольно: пусть U1 = 0. Остальные потенциалы находятся однозначно:

U1 = 0,

V1 = 2, V2 = 4, V5 = 3

U2 = 8 - V2 = 4

U3 = 15 - V2 = 11

V4 = 9 - U3 = -2

V3 = 6 - U2 = 2

Проверяем опорное решение Х1 на оптимальность. С этой целью вычисляем оценки для всех незаполненных клеток таблицы.

∆13 = U1 + V3 - С13 = 0 + 2 – 5 = - 3,

∆14 = U1 + V4 - С14 = 0 - 2 –11 = - 13,

∆21 = U2 + V1 – С21 = 4 + 2 – 12 = - 6,

∆24 = U2 + V4 – С24 = 4 - 2 – 14 = - 12,

∆25 = U2 + V5 – С25 = 4 + 3 – 11 = - 4,

∆31 = U3 + V1 – С31 = 11 + 2 – 10 = 3,

∆33 = U3 + V3 – С33 = 11 + 2 – 7 = 6,

∆35 = U3 + V5 – С35 = 11 + 3 – 18 = - 4.

Начальное опорное решение не является оптимальным, так как имеются положительные оценки.

Переходим к новому опорному решению. Находим клетку таблицы, которой соответствует наибольшая положительная оценка:

 Скачать реферат