Классическое вариационное исчисление. Уравнение Эйлера. Задача вариационного исчисления с подвижными границами
Задание 1
Найти допустимые экстремали в задаче классического вариационного исчисления:
(a) ![]()
Решение:
![]()
Составим уравнение Эйлера
![]() ;
;
Теперь считаем
производные подынтегральной функции по переменным x,![]() , t.
, t.
![]()
![]()
Подставляем полученные значения в уравнение Эйлера
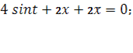
Мы получили неоднородное линейное дифференциальное уравнение 2-ого порядка.
Записываем характеристическое уравнение и ищем его корни
![]()
Поэтому общее решение ищем в виде
![]()
Теперь ищем частное решение:
![]() );
);
![]()
Приравниваем правую и левую части
![]()
Находим неизвестные параметры методом неопределенных коэффициентов
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: ![]() .
.
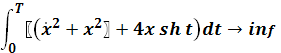 ,
, ![]() ,
, ![]() ;
;
Используем формулу:
![]()
![]()
Решение:
Составим уравнение Эйлера
![]() .
.
![]()
![]()
Уравнение Эйлера принимает вид
Мы получили линейное дифференциальное уравнение второго порядка.
Записываем характеристическое уравнение и находим его корни:
![]() ;
;
Поэтому общее решение ищем в виде
![]()
Подставляем начальные условия:
![]() ;
;
![]()
![]() ;
;
 ;
;
![]()
![]() ,
, ![]() ;
;
Подставляем полученные значения, и получаем следующий ответ:
![]() .
.
Ответ: ![]() .
.
Задание 2
Найдите допустимые экстремали в задаче вариационного исчисления с подвижными границами:
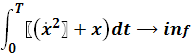 ,
, ![]() ,
, ![]()
Решение:
Составляем уравнение Эйлера
![]() ;
;
![]() ;
;
![]() ;
;
Уравнение Эйлера принимает вид
![]() ;
;
Мы получили неоднородное дифференциальное уравнение второго порядка
![]() ;
;
![]() ;
;
Решим данное уравнение последовательным интегрированием:
![]() ;
;
![]() ;
;
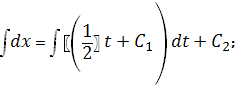
![]() ;
;
Определим неизвестную константу, воспользовавшись начальным условием:
![]()
![]() ;
;
x (T) = ![]()
![]()
![]()
![]()
Ответ: .
.
Задание 3
Решить задачу оптимального управления в форме Лагранжа:
![]()
Решение:
![]()
Записываем задачу в форме Лагранжа, для этого производим замену переменных:
![]()
![]()
![]()
![]()
![]()

![]()
Составляем функцию Гамильтона
Управление достигает своего оптимального значения, если функция Гамильтона достигает максимума.
Найдём такое управление, при котором H достигает max, т.к. управление u не имеет ограничений, воспользуемся достаточным признаком max.
![]() = 0
= 0
![]()
Записываем сопряженную систему:
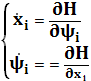
![]()

Другие рефераты на тему «Экономико-математическое моделирование»:
Поиск рефератов
Последние рефераты раздела
- Выборочные исследования в эконометрике
- Временные характеристики и функция времени. Графическое представление частотных характеристик
- Автоматизированный априорный анализ статистической совокупности в среде MS Excel
- Биматричные игры. Поиск равновесных ситуаций
- Анализ рядов распределения
- Анализ состояния финансовых рынков на основе методов нелинейной динамики
- Безработица - основные определения и измерение. Потоки, запасы, утечки, инъекции в модели
