Экономический анализ характеристик взаимосвязи

3.2 Разложение коэффициента множественной детерминации на коэффициенты отдельной детерминации

Для определения доли влияния каждого фактора на показатель используют коэффициенты отдельной детерминации.

Коэффициентом отдельной детерминации для фактора называется произведение коэффициента корреляции между фактором и показателем У на стандартизованный параметр регрессии :

,

Сумма коэффициентов отдельной детерминации равняется коэффициенту множественной детерминации:

Во время анализа двухфакторной модели коэффициенты отдельной детерминации рассчитываются по формулам:

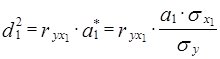
Теперь рассчитаем коэффициенты отдельной детерминации по этим формулам. Полученное значение совпало с тем, которое рассчитали ранее.

Таблица 5 – Расчет коэффициентов отдельной детерминации

3.3 Предварительные выводы об адекватности модели

С помощью полученных коэффициентов множественной детерминации, корреляции и отдельной детерминации можно сделать предварительные выводы об адекватности модели.

1)Поскольку коэффициент множественной детерминации R =0,2126,то это свидетельствует про то, что вариация общих затрат на предприятиях на 21,26% определяется вариацией затрат оборота и трудоемкостью и на 78,74% вариацией показателей, которые не учитываются в модели.

2)Поскольку коэффициенты отдельной детерминации d1=0,2153, определяется вариацией затрат оборота.,027,то это свидетельствует о том, что вариация общих затрат на предприятиях на 21,53% определяется вариацией затрат3)Коэффициент множественной корреляции R =0,2126 характеризует слабую связь между общими затратами и факторами, которые их обуславливают. оборота.

4. Оценка дисперсионно-ковариационной матрицы оценок параметров модели

4.1 Оценка дисперсии отклонений

Вычислим оценку дисперсии отклонений по формуле ,

где - сумма квадратов отклонений;

n – количество наблюдений;

m – количество факторов модели.

Полученное значение проверим копированием с итогового листа Регрессии значение ячейки Остаток с таблицы дисперсийного анализа. Значения совпали.

Таблица 6 – Оценка дисперсии остатков

4.2 Расчет дисперсии и ковариации оценок параметров модели

Для получения оценок ковариаций и дисперсий оценок параметров модели необходимо сложить ковариационную матрицу по формуле:

Таблица 7 – Оценка ковариационной матрицы оценок параметров модели

Мы получили дисперсии оценок параметров модели, которые расположены по главной диагонали:

4.3 Вычисление стандартных ошибок параметров и выводы о смещенности оценок параметров модели

Стандартные ошибки параметров модели рассчитаем по формуле , , . Для получения стандартной ошибки оценки параметров а0 введем формулу возведения в степень 0,5. И аналогично получим стандартные ошибки оценок параметров а1 и а2. Для проверки полученных ошибок скопируем с итогового листа Регрессия значения ячеек столбца Стандартная ошибка. Значения совпали.

Сравним каждую стандартную ошибку с соответствующим значением оценки параметра с помощью формулы:

Таблица 8 – Расчет стандартных ошибок оценок параметров модели. Выводы о смещении оценок параметров модели

 Скачать реферат