Математические модели в экономике

Найдем среднее арифметическое

Среднее квадратическое отклонение

Аномальный уровень отсутствует.

Методом простой скользящей средней с интервалом сглаживания 3

Для вычисления сглаженных уровней ряда применяется формула:

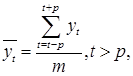
где при нечетном m, в нашем случае m = 3, следовательно

Методом экспоненциального сглаживания (=0,1)

Экспоненциальное сглаживание осуществляется по формуле:, где - параметр сглаживания. В нашем случае = 0,1.

Графическое представление результатов сглажевания

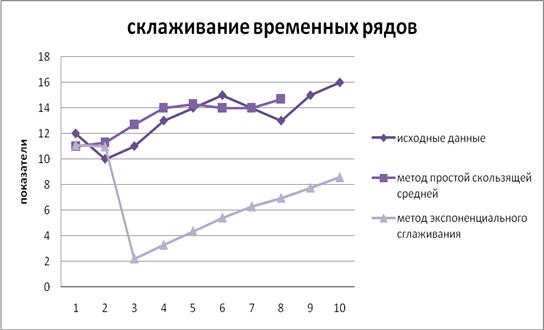
Ниже в таблице приведены исходный ряд данных yt и сглаженные двумя способами уровни исходного ряда. При этом при сглаживании при помощи метода простой скользящей средней использовался интервал сглаживания m = 3.

При сглаживании экспоненциальным методом был доведён параметр сглаживания а = 0,1

Соответственно, числовая последовательность весов имела вид:

Чтобы правильно подобрать лучшую кривую роста для моделирования и прогнозирования экономического явления, необходимо знать особенности каждого вида кривых в экономике часто используется полиномиальная кривая роста, как кривая с полиномом первой степени.

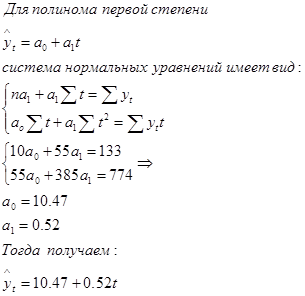
Параметр a1 называют линейным приростом. Для полинома первой степени характерен постоянный закон роста. Если посчитать первые приросты по формуле

ut = yt – yt-1, t = 2,3,…,n,

то они будут постоянной величиной и равны а 1.

Значения прироста для полиномов любого порядка не зависят от значений самой функции .

Полиномные кривые роста можно использовать для аппроксимации (приближения) и прогнозирования экономических процессов, в которых последующее развитие не зависит от достигнутого уровня. Исходный временной ряд предварительно сглаживается методом простой скользящей средней.

 Скачать реферат