Системы, эквивалентные системам с известными качественными свойствами решений
Пусть имеется дифференциальная система
![]()
![]()
с правой частью, удовлетворяющей теореме существования и единственности. Предположим, что функция ![]() является первым интегралом с
является первым интегралом с
истемы ![]() .
.
Теорема 5.1. Дифференциальная система
![]()
![]()
в которой ![]() нечётная скалярная функция, а функция
нечётная скалярная функция, а функция ![]() является непрерывно дифференцируемой функцией, имеет ту же отражающую функцию что и система
является непрерывно дифференцируемой функцией, имеет ту же отражающую функцию что и система ![]()
Доказательство. Правую часть системы ![]() обозначим
обозначим ![]() . Положим,
. Положим, ![]() и покажем, что функция
и покажем, что функция ![]() удовлетворяет уравнению
удовлетворяет уравнению
![]()
![]()
Находим ![]()
![]() . Подставим эти выражения в левую часть уравнения
. Подставим эти выражения в левую часть уравнения ![]() . Получим
. Получим
![]()
Выражение ![]() в силу определения интеграла системы и, следовательно, функция
в силу определения интеграла системы и, следовательно, функция ![]() действительно удовлетворяет уравнению
действительно удовлетворяет уравнению ![]() . Согласно теореме 2 [см.5] системы
. Согласно теореме 2 [см.5] системы ![]() и
и ![]() эквивалентны.
эквивалентны.
Из теоремы вытекают следующие замечания:
Замечание 5.1. Известно, что если дифференциальная система ![]() эквивалентна некоторой стационарной, то она эквивалентна и системе
эквивалентна некоторой стационарной, то она эквивалентна и системе ![]() [3, с.24; 4, с.79]. Положив
[3, с.24; 4, с.79]. Положив ![]() , и используя утверждение теоремы 5.1, мы построим нестационарную дифференциальную систему, эквивалентную
, и используя утверждение теоремы 5.1, мы построим нестационарную дифференциальную систему, эквивалентную ![]() .
.
Замечание 5.2 Особый интерес представляет построение нестационарных систем, эквивалентных хорошо исследованной стационарной. Приведём пример такого построения. Как известно исследованию стационарных дифференциальных систем посвящено огромное количество работ. Это объясняется тем, что эти системы во многих отношениях являются более просто исследуемыми чем неавтономные системы. Если различные дифференциальные системы имеют одну и ту же отражающую функцию, то значит они имеют одно и то же отображение за период в том случае, когда эти системы периодичны. При этом следует учитывать, что качественное поведение решений дифференциальных систем с одной и той же отражающей функцией одинаково.
Рассмотрим дифференциальную систему
![]()
![]()
![]()
которая имеет, в зависимости от знака ![]() , асимптотически устойчивый или неустойчивый предельный цикл
, асимптотически устойчивый или неустойчивый предельный цикл ![]() .
.
Справедлива следующая
Теорема 5.2. Дифференциальная система

![]()
в которой
![]() ,
, ![]() ,
,
функции ![]() ,
, ![]() непрерывные нечётные, вектор функции
непрерывные нечётные, вектор функции
![]() ,
, 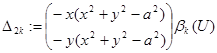 ,
,
где ![]()
и функции ![]() и
и ![]() непрерывно дифференцируемы, имеет ту же отражающую функцию, что и система
непрерывно дифференцируемы, имеет ту же отражающую функцию, что и система ![]() .
.
Доказательство. Правую часть системы ![]() обозначим
обозначим ![]() и положим
и положим
![]() .
.
Проверим для указанного ![]() выполнение равенства
выполнение равенства
![]() .
.
Находим
![]()
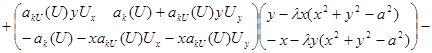
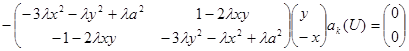
Здесь учтены равенства
![]()
![]()
![]()
Аналогичным образом легко убедиться, что и ![]() является решением уравнения
является решением уравнения
![]() .
.
Действительно
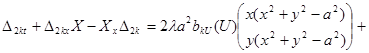
![]()

Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
