Системы, эквивалентные системам с известными качественными свойствами решений

В соответствии с теоремой 1 [5, с.1326] добавка к правой части системы слагаемых и не изменяет её отражающей функции.

Теорема доказана.

Теорема 5.3. Пусть в с

истеме функции и периодичны. Тогда все решения этой системы, начинающиеся при на окружности , являются периодическими. Все остальные решения, кроме тривиального, при либо стремятся к одному из указанных периодических, либо уходят от них в зависимости от знака .

Замечание 5.3. Если правая часть системы представляет собой многочлены от искомых функций и известен полиномиальный первый интеграл такой системы, то с помощью указанной теоремы легко строится система с полиномиальной правой частью степень многочленов которой выше, чем в исходной системе. Следует отметить также и возможность решения обратной задачи. Пример решения такого типа задачи приведём ниже.

Рассмотрим уравнения

Здесь нечётная функция .

Правую часть уравнения обозначим . Положим

и подберём функции и так, чтобы функция удовлетворяла уравнению , при этом учитываем, что функции и известны.

Лемма 5.1. Если функция удовлетворяет уравнению , то выполняются равенства

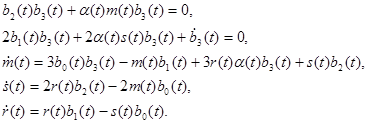
Доказательство: Вычислим , , . Получим

Подставим полученные выражения в уравнение , получим:

Раскрывая скобки и приравнивая коэффициенты при одинаковых степенях к , получаем:

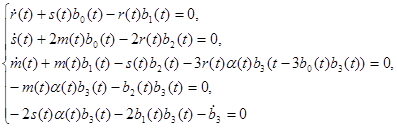
Выражая из первого, второго и третьего уравнений системы , , соответственно и умножая четвёртое и пятое уравнения системы на получаем то, что требовалось доказать.

Лемма доказана.

Лемма 5.2. Пусть функции и обращаются в нуль лишь в отдельных точках, в которых функции доопределены до непрерывной дифференцируемости. Тогда

,

Доказательство: Рассмотрим более подробно четвёртое уравнение системы

Или

Поскольку по условию леммы , то сократим обе части равенства на . Получим: .

Поскольку и функцию можно определить до непрерывно-дифференцируемой, то (это следует из последнего равенства) удовлетворяет равенствам из условия леммы 5.1.

Аналогично, из пятого уравнения системы

.

Лемма доказана.

Лемма 5.3. Пусть функция обращается в нуль лишь в изолированных точках, в которых функции , , где функции , определяется формулой , доопределены до непрерывной дифференцируемости. Тогда

 Скачать реферат