Системы, эквивалентные системам с известными качественными свойствами решений

Необходимость. Пусть есть первый интеграл системы . Тогда для любого решения этой системы, применяя лемму 1 будем иметь тождества

откуда при получим равенство справедливое при всех значениях и . Необходимость доказана.

Достаточность. Пусть теперь при всех Тогда для любого решения системы на основании леммы1 будем иметь тождество

а с ним и достаточность.

Лемма доказана.

Из определения первого интеграла следует, что постоянная на функция также является первым интегралом системы . Первый интеграл будем называть невырожденным на , если при всех выполняется неравенство

Функцию будем называть стационарным первым интегралом системы , если она не зависит от и является первым интегралом системы .

Теорема 4.1. Для того, чтобы система с раз дифференцируемой по правой частью имела в невырожденный стационарный первый интеграл, необходимо выполнение тождества

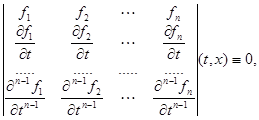
где , компоненты вектор-функции .

Доказательство. Пусть стационарный первый интеграл системы . Тогда согласно лемме 4.2 должно выполняться тождество

Это означает, что при каждом фиксированном функции линейно зависимы на интервале их существования. Поэтому вронскиан этих функций (левая часть тождества ) обязан обращаться в нуль.

Теорема доказана.

Выясним условия, при которых система имеет стационарный интеграл. Будем считать, что условия теоремы 4.1 выполнены. Составим систему линейных уравнений относительно неизвестных функций

………………………………………….

Теорема 4.2. Для того, чтобы система с раз дифференцируемой по правой частью имела хотя бы один стационарный интеграл , необходимо и достаточно существование такого независящего от решения системы , для которого уравнение Пфаффа

интегрируется одним соотношением .

Необходимость. Пусть система имеет стационарный интеграл . Тогда согласно лемме 4.2 должно выполняться тождество . Дифференцируя тождество раз по , убеждаемся в том, что совокупность функций решение системы .

 Скачать реферат