Математические методы оптимизации

для базисных переменных . Следовательно, базисное решение имеет вид . Это базисное решение означает, что изделия А производится 60 ед., изделие В не производится, не хватает времени обработки 168

0 минут для первой линии, а время обработки второй линии используется полностью. Это базисное решение не является допустимым.

6) Пусть свободные переменные. Тогда базисные переменные и найдём из системы уравнений

Отсюда следует, что базисное решение имеет вид . Это решение означает, что изделия А производятся в количестве ед., изделия В производятся в количестве , время обработки на каждой из линий используется полностью. Это базисное решение является допустимым. Выручка от реализации составит ден.ед.

· Определим оптимальное базисное решение.

Из теории линейного программирования следует, что оптимальное решение можно найти среди допустимых базисных решений. Отсюда следует, что для определения оптимального решения нужно вычислить значения целевой функции на всех допустимых базисных решениях. Оптимальным будет базисное решение, на котором значение целевой функции наибольшее.

В таблице 1.1 приведены все допустимые базисные решения и соответствующие им значения выручки .

двойственный задача равновесный спрос полезность товар

Таблица 1.1

Максимальное значение выручки достигается на четвёртом базисном решении в этой таблице

Следовательно, изделие А производится в количестве ед., изделие В производится в количестве ед., время обработки на каждой из линий используется полностью ().

Графическое решение задачи

Рассмотрим задачу в стандартной форме: найти переменные , которые обеспечивают максимальное значение функции

при ограничениях

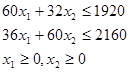
На горизонтальной оси прямоугольной системы координат будем откладывать план выпуска продукции , а на вертикальной – план выпуска второй продукции .

Рассмотрим первое ограничение . Множество точек, удовлетворяющих равенству , образует прямую на плоскости. Построим эту прямую по её точкам пересечения с осями координат. Для определения координат точки А пересечения с осью в уравнение подставим . Из него следует , т.е . Для определения координат точки В пересечения с осью в уравнение подставим . Из него следует , т.е. . Неравенству удовлетворяют все точки одной из полуплоскостей, которые образовала построенная прямая. Для её определения достаточно проверить справедливость неравенства для одной точки. Для начала координат неравенство выполняется. Следовательно, все точки полуплоскости, содержащей начало координат, будут графическим изображением этого неравенства. Аналогично построим прямую по её точкам пересечения с осями координат: . Все точки полуплоскости, содержащей начало координат будут графическим изображением неравенства . Учитывая ограничения на знак , множество точек четырёхугольника является множеством всех допустимых решений. Все угловые точки (крайние точки) четырёхугольника соответствуют допустимым базисным решениям:

 Скачать реферат