Математические методы оптимизации

2. Найдём частные производные функции полезности

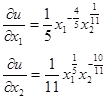
Предельная полезность первого товара в наборе равна значению частной производной в точке (3,8):

.

Предельная полезность второго товара в наборе равна значению частной производной в точке (3,8):

Найдём изменение полезности, если количество первого товара увеличивается на 0,1, т.е. , а количество второго товара уменьшается на 0,2, т.е. . Приближённое изменение полезности вычислим по формуле

.

Следовательно, полезность набора , равная , увеличивается на 0,0065. Таким образом, полезность нового набора

Задание 4. Модель Стоуна

Функция полезности потребителя имеет вид

, где

.

1. Найти равновесный спрос и его полезность, если рыночная цена первого товара , рыночная цена второго товара и потребитель выделяет на приобретение товаров сумму денежных единиц.

2. Найти функции спроса на оба вида товаров.

3. Найти спрос на оба товара при увеличении дохода на 30 денежных единиц и при уменьшении дохода на 60 денежных единиц.

РЕШЕНИЕ

1. Функция полезности потребителя имеет вид

.

Вычислим равновесный спрос при заданных ценах и доходе. Найдём стоимость минимального набора товаров

.

Оставшаяся сумма денег распределяется пропорционально коэффициентам эластичности этих товаров

.

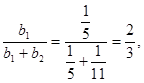
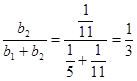На приобретение первого товара выделяется сумма

.

На приобретение 2-го товара - сумма

.

Поделив выделенные средства на рыночные цены товаров, получаем количество товара, приобретаемое сверх установленных нормативов

Таким образом, оптимальный спрос составит

единиц первого товара и

единиц второго товара.

Полезность равновесного набора будет равна

.

2. Найдём функции спроса, заменяя в формулах спроса

, .

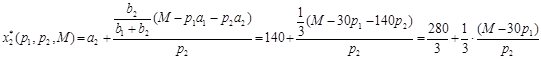
Эти формулы определяют спрос на продукцию при любых ценах и доходах.

3. Оценим влияние на спрос изменения дохода обоих товаров. Найдём реакцию спроса на изменение дохода на 1 денежную единицу. Частные производные по доходу 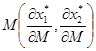показывают изменение спроса на первый и второй товары соответственно при возрастании дохода на 1 денежную единицу.

Дифференцируя полученные выше функции спроса по М, получаем

.

Вычислим эти частные производные при заданных и :

.

Так как значения частных производных положительные, то оба товара являются ценными: с ростом дохода на 1 денежную единицу спрос на оба товара растёт: спрос на первый товар увеличивается на , а второго - на .

При увеличении дохода потребителя на 30 денежных единиц спрос на первый товар увеличится на единицы, а второго на и составит

, .

При уменьшении дохода потребителя на 60 денежных единиц спрос на первый товар снизится на единиц, а спрос на второй товар снизится на единиц и составит соответственно:

, .

Размещено на Allbest.ru

 Скачать реферат