Математические методы оптимизации
![]()
при ограничениях

Переменные Экономический смысл двойственной задачи:
двойственная переменная Тогда целевая функция Выражение Определим величины приведённых стоимостей.
Если величина Отсюда следует, что при допустимых теневых ценах Можно дать следующую экономическую интерпретацию двойственной задачи. Некоторая фирма предлагает производителю продукции продать ей все запасы ресурсов по теневым ценам Найдём оптимальное решение двойственной задачи
Из первого задания следует, что допустимое базисное решение
является оптимальным решением прямой задачи.
По оптимальному базисному решению Из этих равенств найдём оптимальные значения двойственных переменных Оптимальная теневая цена работы 1 минуты оборудования линии 1 равна Стоимость работы технологического оборудования, затраченных на изготовление единицы изделия А равна
а стоимость работы технологического оборудования, затраченных на изготовление единицы изделия В равна
Приведённые стоимости каждого вида изделия будут раны
Отсюда следует, что производство изделий А и В рентабельно.
Определим целесообразность производства продукции С, для которой на изготовление единицы продукции требуется 60 минут и 50 минут времени изготовления на первой и второй линии соответственно. Рыночная цена составляет 120 ден. ед. за единицу продукции. Для этого вычислим стоимость ресурсов, затраченных на изготовление единицы продукции С:
Приведённая стоимость этого вида продукции будет равна
Отсюда следует, что производство единицы продукции С принесёт прибыль Задание 3. Функция полезности
Пусть функция полезности наборов из двух товаров · Найти набор товаров, который имеет такую же полезность, как набор · Для набора · В наборе РЕШЕНИЕ
1. Функция полезности имеет вид: Кривая безразличия ![]() , называются допустимым решением двойственной задачи, если они удовлетворяют всем ограничениям и оптимальными, если они допустимые и на них целевая функция
, называются допустимым решением двойственной задачи, если они удовлетворяют всем ограничениям и оптимальными, если они допустимые и на них целевая функция ![]() определяет теневую цену работы 1 минуты оборудования линии 1, а двойственная переменная
определяет теневую цену работы 1 минуты оборудования линии 1, а двойственная переменная ![]() определяет теневую цену работы 1 минуты оборудования линии 2.
определяет теневую цену работы 1 минуты оборудования линии 2.
![]() задаёт стоимость времени работы оборудования в теневых ценах соответственно для линии 1 и линии 2.
задаёт стоимость времени работы оборудования в теневых ценах соответственно для линии 1 и линии 2.
![]() определяет стоимость 60 минут и 36 минут, затраченных на изготовление единицы изделия А в теневых ценах, а выражение
определяет стоимость 60 минут и 36 минут, затраченных на изготовление единицы изделия А в теневых ценах, а выражение ![]() определяет стоимость 32 минут и 60 минут, затраченных на изготовление единицы изделия В в теневых ценах.
определяет стоимость 32 минут и 60 минут, затраченных на изготовление единицы изделия В в теневых ценах.
![]()
![]() положительна, то стоимость ресурсов больше рыночной цены этого продукта. В этом случае производство продукта убыточно. Если величина
положительна, то стоимость ресурсов больше рыночной цены этого продукта. В этом случае производство продукта убыточно. Если величина ![]() отрицательна, то стоимость ресурсов меньше рыночной цены этого продукта. Если величина
отрицательна, то стоимость ресурсов меньше рыночной цены этого продукта. Если величина ![]() равна 0, то стоимость ресурсов равна рыночной цене. Ограничения двойственной задачи
равна 0, то стоимость ресурсов равна рыночной цене. Ограничения двойственной задачи

![]() производство обоих продуктов неприбыльно.
производство обоих продуктов неприбыльно.
![]() и
и ![]() . Решение двойственной задачи определяет минимальный уровень рыночных цен
. Решение двойственной задачи определяет минимальный уровень рыночных цен ![]() , при котором производить продукцию неприбыльно.
, при котором производить продукцию неприбыльно.
![]()
![]() прямой задачи найдём оптимальное решение двойственной. Для этого все ограничения двойственной задачи, соответствующие базисным переменным
прямой задачи найдём оптимальное решение двойственной. Для этого все ограничения двойственной задачи, соответствующие базисным переменным ![]() нужно заменить равенствами
нужно заменить равенствами

![]() , минимальное значение целевой функции равно
, минимальное значение целевой функции равно
![]() .
.
![]() , а оптимальная теневая цена 1 минуты оборудования линии 2 равна
, а оптимальная теневая цена 1 минуты оборудования линии 2 равна ![]() .
.
![]() ,
,
![]() .
.
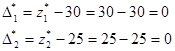
![]() ден. ед.
ден. ед.
![]() .
.
![]() ден. ед.
ден. ед.
![]() имеет вид
имеет вид ![]() , где
, где
![]() .
.
![]() и количество второго товара равно 1.
и количество второго товара равно 1.
![]() найти предельные полезности первого и второго товаров.
найти предельные полезности первого и второго товаров.
![]() количество первого товара увеличивается на 0,1, а второго уменьшается на 0,2. Найти приближённое изменение полезности.
количество первого товара увеличивается на 0,1, а второго уменьшается на 0,2. Найти приближённое изменение полезности.
![]() . Найдём полезность набор
. Найдём полезность набор ![]() :
:
![]()
![]() определяет все наборы товаров, которые имеют такую же полезность как набор
определяет все наборы товаров, которые имеют такую же полезность как набор ![]() . Из этого уравнения можно найти набор товаров, в котором количества второго товара равно
. Из этого уравнения можно найти набор товаров, в котором количества второго товара равно ![]() , подставив это значение в уравнение кривой безразличия
, подставив это значение в уравнение кривой безразличия ![]() ,
, ![]() . Таким образом, наборы
. Таким образом, наборы ![]() и
и ![]() безразличны для потребителя.
безразличны для потребителя.
Другие рефераты на тему «Экономико-математическое моделирование»:
Поиск рефератов
Последние рефераты раздела
