Комплексный анализ рыбной отрасли
Из пары факторов х3 и х2 исключаем фактор х2, так как его связь с другими факторами более сильная, чем связь x3 с ними. Исключаем фактор x7, так как его связь с y очень незначительная. По такой схеме исключаем все другие факторы. Таким образом, для построения модели остаются факторы х1, х5, х8 и х10. Матрица коэффициентов парной корреляции для них выглядит следующим образом:
|
у |
х1 |
х5 |
х8 |
х10 | |
|
у |
1 | ||||
|
х1 |
-0,88300608 |
1 | |||
|
х5 |
0,45605173 |
-0,003474 |
1 | ||
|
х8 |
0,59499201 |
-0,342415 |
0,619844 |
1 | |
|
х10 |
-0,635065 |
0,297207 |
-0,685489 |
-0,6729266 |
1 |
Для получения адекватной модели необходимо устранить мультиколлинеарность, т.е. вывести из рассмотрения факторы, которые имеют совокупное воздействие друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые из них всегда будут действовать в унисон. Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Чем ближе к нулю этот проеделитель, тем сильнее мультиколлинеарность факторов. Для наших парных коэффициентов корреляции между факторами матрица имеет вид:
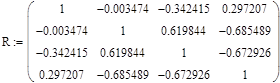
![]()
Определитель матрицы парных коэффициентов корреляции между факторами равен 0,2, что достаточно близко к 0, следовательно, между оставшимися факторами наблюдается мультиколлинеарность.
Продолжим удаление факторов, являющихся самыми неинформативными, регулярно сопоставляя значения множественного коэффициента корреляции и детерминации (который оценивает качество построенной модели в целом) и проверяя значимость уравнения регрессии.
В следующих таблицах представлены результаты регрессионного анализа после исключения факторов х1, х5, х8, х10.
|
ВЫВОД ИТОГОВ | |
| Регрессионная статистика | |
|
Множественный R |
0,999530603 |
|
R-квадрат |
0,999061427 |
|
Нормированный R-квадрат |
0,995307133 |
|
Стандартная ошибка |
29,05134237 |
|
Наблюдения |
6 |
|
Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
|
Регрессия |
4 |
898372,4 |
224593,0982 |
266,111717 |
0,045939839 |
|
Остаток |
1 |
843,9805 |
843,9804935 | ||
|
Итого |
5 |
899216,4 |
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | |
|
Y-пересечение |
30538,08691 |
1623,46624 |
18,81042319 |
0,03381216 |
|
x1 |
-26,94728304 |
1,07745261 |
-25,01017937 |
0,02544087 |
|
x5 |
0,007316604 |
0,00087595 |
8,352752758 |
0,07585572 |
|
x8 |
-242,9957642 |
101,983594 |
-2,382694665 |
0,25297163 |
|
x10 |
-81,66075105 |
21,2523898 |
-3,842426757 |
0,16208611 |
Другие рефераты на тему «Экономико-математическое моделирование»:
Поиск рефератов
Последние рефераты раздела
- Выборочные исследования в эконометрике
- Временные характеристики и функция времени. Графическое представление частотных характеристик
- Автоматизированный априорный анализ статистической совокупности в среде MS Excel
- Биматричные игры. Поиск равновесных ситуаций
- Анализ рядов распределения
- Анализ состояния финансовых рынков на основе методов нелинейной динамики
- Безработица - основные определения и измерение. Потоки, запасы, утечки, инъекции в модели
