Радиолокационные установки

, (1.22)

Где

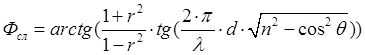, (1.23)

.

Таким образом, диэлектрический слой влияет не только на амплитуду проходящей сквозь него волны, но и на фазу. [21]

1.3 Дифрак

ция радиоволн

Явление дифракции позволяет радиоволнам распространяться вокруг сферической земной поверхности за горизонт и за различные препятствия. Несмотря на перекрытие прямой видимости и существенное уменьшение уровня сигнала, он все таки остается достаточным для приема.

Феномен дифракции объясняется принципом Гюйгенса - вторичного переизлучения точек фронта волны с различной фазой (зон Френеля). Напряженность поля определяется векторной суммой вклада вторичных излучателей.

1.3.1 Геометрия зон Френеля

Пусть между излучателем и приемником расположено препятствие - экран высотой h бесконечных размеров в поперечном сечении. Расстояние от экрана до излучателя - d1, до приемника - d2.

Рис.1.5 Дифракция радиоволн на клиновидном препятствии

Ясно, что путь через кромку препятствия больше прямого. Полагая, что h<<d1,d2 и h>>l, разность хода прямого и через кромку лучей будет:

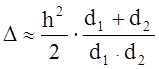. (1.27)

Соответствующая ему разность фаз

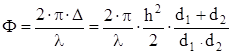, (1.28)

где используется приближение для малого аргумента tg x » x, а угол a аппроксимирован выражением

.

Выражение (1.28) может быть аппроксимировано с использованием безразмерного дифракционного параметра Френеля - Кирхгофа:

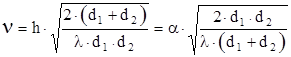, (1.29)

где a подставляется в радианах, все остальные параметры - в метрах. Таким образом, разность фаз Ф может быть вычислена из выражения

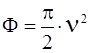. (1.30)

Из выражения (1.30) следует, что сдвиг фазы между прямым и дифракционным лучами является функцией высоты h и взаимного расположения препятствия, излучателя и приемника.

Дифракционные потери мощности в радиоканале могут быть объяснены с помощью зон Френеля. Зоны Френеля представляют собой области, разность хода через которые от излучателя до приемника составляет nl/2 по сравнению с прямым лучом (l - длина волны, n - целое число).

В мобильной связи обычно наблюдается затенение части зон (источников вторичных волн) и, следовательно, уменьшение доли принятой мощности. В зависимости от геометрии препятствия принятая энергия определяется через векторное суммирование вторичных волн.

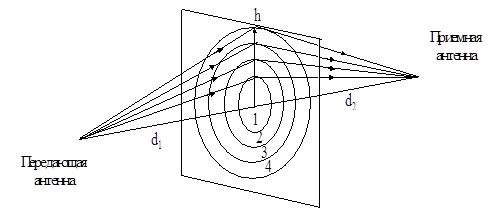
Рис.1.6 Формирование зон Френеля

Если препятствие не затеняет первую зону Френеля, то дифракционные потери минимальны и ими пренебрегают. Используют следующее свойство: если открыто не менее 55% первой зоны Френеля, то дальнейшее открытие первой зоны Френеля не уменьшает дифракционные потери.

1.3.2 Модель дифракции радиоволн на одиночном клине

Определение степени ослабления поля холмами и зданиями является достаточно сложной задачей при расчете зон обслуживания. Обычно точный расчет ослабления невозможен, поэтому используют методы расчета поля с необходимыми экспериментальными поправками.

Препятствие в виде одиночного холма или горы может быть обсчитано с использованием модели клина. Это простейшая модель препятствия, и быстрый расчет ослабления возможен с использованием классического решения Френеля для дифракции поля на полуплоскости.

Рис.1.7 Варианты перекрытия видимости антенн препятствием

Напряженность поля в точке расположения приемной антенны определяется векторной суммой вторичных источников, лежащих в плоскости, расположенной над препятствием. Напряженность поля при дифракции на клине определяется выражением

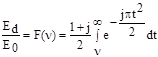, (1.31)

где Е0 - напряженность поля в точке расположения приемной антенны при отсутствии препятствия и земли, а F (n) - комплексный интеграл Френеля. Значение интеграла F (n) определяется из графиков и таблиц.

Коэффициент дифракционного усиления с препятствием (обычно он меньше 1) по сравнению со свободным пространством

, дБ. (1.32)

График этой функции показан на рис.1.8

Gd, дБn

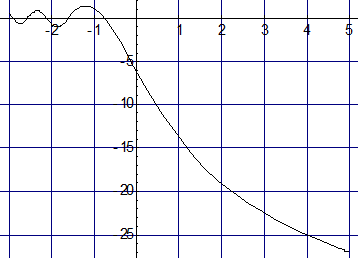
Рис.1.8 Зависимость коэффициента дифракционного усиления от значения параметра дифракции n

Приближенно можно считать:

(1.33a)

(1.33б)

(1.33в)

(1.33г)

(1.33д)

1.3.3 Дифракция на нескольких клиньях

Если на пути между излучателем и приемником имеется несколько препятствий, то все они аппроксимируются одним эквивалентным препятствием (рис.1.9).

Рис.1.9 Эквивалентное клиновидное препятствие в задаче связи с двумя препятствиями

Эта модель хорошо работает для двух препятствий, для нескольких - возникают определенные математические трудности.

1.4 Рассеяние радиоволн

Потери от рассеяния радиоволн на препятствиях обычно много меньше потерь отражения и дифракции. Это объясняется тем, что рассеяние волн происходит во всех направлениях (на таких объектах, как мачты, лампы, деревья и т.д.).

Плоские поверхности с размерами много больше длины волны могут моделироваться как отражающие поверхности. Однако наличие неровностей изменяет отражение. Неровность поверхности определяется критерием Релея, который определяет критическую высоту hc неровностей при падении волны под углом qi:

. (1.34)

Поверхность считается гладкой, если разброс минимальных и максимальных высот меньше hc. Для неровных поверхностей коэффициент отражения r умножается на коэффициент потерь рассеяния ps.

Полагая, что высота неровностей h распределена случайным образом с гауссовым законом распределения, коэффициент потерь рассеяния

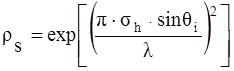, (1.35)

 Скачать реферат