Проектирование судов
Дифференциальные уравнения масс
В отличие от алгебраических, дифференциальные уравнения масс не дают ответ на вопрос, какими должны быть элементы проектируемого судна согласно требованиям задания на проектирование. С помощью дифференциальных уравнений определяют, каким образом необходимо изменить элементы прототипа, чтобы выполнить требования, предъявляемые к проекту. Обычно,
предполагают, что изменение независимых переменных и элементов судна – это достаточно малые величины, так как в противном случае замена конечных приращений дифференциалами будет приводить к большой погрешности.
Допустим, что какой-либо из разделов нагрузки выражается формулой
Р = рХn,
где Х – какой-то элемент судна, причем для прототипа Р = Р0, Х = Х0. Масса этого же раздела проектируемого судна составит Р = рХn = Р0 + dP, где dP – приращение массы этого раздела. Для нахождения dP продифференцируем исходную формулу.
dР = (рХn)' dX = nрХn - 1 dX = n![]() dX.
dX.
C другой стороны для проектируемого судна масса раздела составит
Р = р(Х0 + dХ)n.
Разложим это выражение в ряд Маклорена, сохранив первые три члена ряда
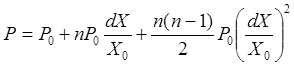 .
.
Тогда
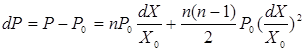 .
.
Два выражения, полученные для dP, отличаются на величину
![]() ,
,
которая характеризует абсолютную погрешность метода. Относительная погрешность ε/Р0 будет зависеть от соотношения dХ/Х и степени n и при различных значениях этих показателей будет иметь следующие значения.
При использовании дифференциальных уравнений считается, что погрешность не выходит из допустимых пределов, если изменения параметров проекта, по отношению к прототипу, не превосходит следующих значений: скорость хода – 4 - 5 %, главные размерения – 7 - 10 %, водоизмещение до 20 %.
|
dХ/Х |
Относительная погрешность ε/Р0, % | ||||
|
n = 3,0 |
n = 2,0 |
n = 1,0 |
n = 2/3 |
n = 0,5 | |
|
0,05 0,10 0,20 |
0,75 3,0 12,0 |
0,25 1,0 4,0 |
0 0 0 |
0,03 0,11 0,45 |
0,03 0,12 0,50 |
Обобщенное дифференциальное уравнение масс
Алгебраическое уравнение масс перепишем в виде
Р = D – ΣРi(δ, L, B, H, T, υs, r, a, b,…) = D – F,
где, как и прежде ΣРi = F – массы зависимые от размерений, коэффициентов полноты, скорости, дальности плавания и прочих независимых переменных, Р – независимые массы. Дифференцируя это уравнение, получим
dР = dD – dF,
и раскроем dD и dF как полные дифференциалы по всем независимым переменным, т.е. по δ, L, B, H, T, υs, r, a, b, c….
выражение для dD будет выглядеть следующим образом:
![]() .
.
Найдем частные производные.
![]() .
.
Подобным же образом можно вывести, что ![]() ,
, ![]() ,
, ![]() . Тогда
. Тогда
![]() .
.
Аналогично можно написать, что
![]()
![]()
Введем обозначение
![]() ,
,
то есть полный дифференциал функции F по всем переменным, исключая главные размерения и коэффициент полноты.
Окончательный вид уравнения масс в этом случае примет вид
![]()
![]() .
.
Величины, стоящие в левой части уравнения, должны, очевидно, рассматриваться как заданные. Соответственно заранее необходимо определить полный дифференциал функции F по независимым переменным. Так же определяются и искомые частные производные по главным размерениям и коэффициенту полноты. Отношение водоизмещения к главным размерениям и коэффициенту полноты принимается по прототипу.
Для вычисления частных производных функции F надо найти частные производные каждого из разделов входящих в F по каждой из переменных δ, L, B, H, T. Например, пусть какой-нибудь из разделов выражается зависимостью
Рi = pi δmLnBkHxTy,
в которой степени могут быть целыми или дробными, положительными или отрицательными.
Частная производная Рi по коэффициенту полноты
![]() .
.
Величину этой частной производной можно вычислить по прототипу. Частная производная функции F определяется как сумма частных производных отдельных разделов.
![]() .
.
Очевидно, что частные производные по другим переменным будут определяться подобным же образом.
Поскольку в полученном уравнении фигурируют пять неизвестных, то для решения уравнения необходимо задаться дополнительными зависимостями, для выражения одного элемента через другой. Это могут быть либо уравнения теории корабля, либо ограничения размерений, либо соотношение размерений прототипа. Последний способ выражения главных размерений является наиболее употребительным. В этом случае
![]() ,
,
откуда
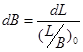 .
.
Аналогично выражаются и прочие приращения главных размерений. Коэффициент общей полноты задают исходя из статистических зависимостей, или принимают по прототипу. В первом случае dδ = δ – δ0, во втором dδ = 0.
Дифференциальное уравнение масс Бубнова
От обобщенного дифференциального уравнения масс уравнение Бубнова отличается тем, что второе слагаемое левой части [dF]0 = 0. Для учета изменения скорости хода, дальности плавания, измерителей и прочих независимых переменных И.Г.Бубнов предложил пересчитывать элементы проектируемого судна не относительно элементов прототипа, а относительно элементов какого-то судна, имеющего главные размерения и коэффициенты полноты прототипа, но независимые переменные, соответствующие проектируемому судну. Поскольку такое сочетание у реально существующих судов найти практически невозможно, необходимо изменить нагрузку прототипа, таким образом, чтобы оказались выполненными элементы технического задания проекта. Поскольку после введения изменений нагрузка прототипа не будет соответствовать водоизмещению прототипа, его необходимо компенсировать за счет независимых масс.
Другие рефераты на тему «Транспорт»:
Поиск рефератов
Последние рефераты раздела
- Проект пассажирского вагонного депо с разработкой контрольного пункта автосцепки
- Проектирование автомобильных дорог
- Проектирование автотранспортного предприятия МАЗ
- Производственно-техническая база предприятий автомобильного транспорта
- Расчет подъемного механизма самосвала
- Системы автоблокировки
- Совершенствование организации движения и снижение аварийности общественного транспорта в городе Витебск
