Проектирование судов

Общая формула определения масс разделов исправленного прототипа

.

Изменение масс независимых разделов осуществляется прямым расчетом. Для компенсации получившегося расхождения между нагрузкой и водоизмещением необходимо изменить массу перевозимого прототипом груза.

Обобщенный коэффициент приращения водоизмещения>

Для вывода уравнения будем рассматривать приращение высоты борта как заданную величину. Преобразуем исходное уравнение dP = dD – d(ΣPi) к виду

,

где – полный дифференциал переменных масс по главным размерениям подводной части и коэффициенту полноты. Объедением приращение независимых масс и приращение масс разделов вызванное изменением независимых переменных.

.

Тогда обобщенное дифференциальное уравнение можно записать в виде

.

Если вести обозначение

,

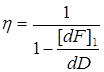где , то обобщенное уравнение можно записать, относительно неизвестного dD, в виде

dD = ηΔ.

Зная численное значение коэффициента η можно определить приращение водоизмещения, соответствующее заданному приращению масс Δ. Но для этого необходимо исключить из уравнения неизвестные приращения элементов. Предположим, что заданное приращение Δ компенсируется за счет приращение только какого-то одного элемента. Пусть dL = dB = dT = 0, dδ ≠ 0.

Тогда

.

Можно составить такие же выражения применительно к другим элементам судна. Аналогично формуле для обобщенного коэффициента запишем формулы для частных случаев

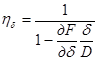для dL = dB = dT = 0, dδ ≠ 0.

для dδ = dB = dT = 0, dL ≠ 0.

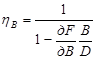для dδ = dL = dT = 0, dB ≠ 0.

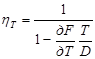для dδ = dL = dB = 0, dT ≠ 0.

Полученные коэффициенты ηδ, ηL, ηB, ηT могут рассматриваться как частные коэффициенты приращения водоизмещения по соответствующим элементам. Для определения приращения водоизмещения в каждом из случаев, по аналогии с общей формулой, можно записать

,

,

,

.

Частные коэффициенты приращения водоизмещения могут быть вычислены для каждого конкретного судна, если известны его элементы и нагрузка.

С точки зрения экономии масс выгоднее всего увеличивать водоизмещение проектируемого судна за счет тех элементов, которым соответствуют минимальным значениям коэффициентов ηi. Минимальное водоизмещение будет у того судна, у которого ηδ = ηL = ηB = ηT. Однако, это практически неосуществимо, поскольку кроме соотношения нагрузок по отдельным разделам, приходится учитывать требования к остойчивости, ходкости, вместимости и пр. Поэтому приходиться говорить не о минимальном, а о минимально возможном водоизмещении судна.

Независимое приращение масс Δ – есть сумма частных приращений.

Δ = Δδ + ΔL + ΔB + ΔT.

Разделив полученное выражение на D, получим, после подстановки значений Δi, следующую формулу

.

Из выражения dD = ηΔ получим формулу для определения η.

.

Или

.

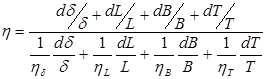Пользуясь этой формулой, легко определить значение коэффициента η для любых частных случаев.

Дифференциальное уравнение масс Нормана

Если алгебраическое уравнение масс, выраженное в функции водоизмещения привести к виду

Р = D – ΣPi(D, υs, r, a, b,…),

в котором, как и раньше а, b – какие-то независимые переменные, то при дифференцировании, с учетом выведенных ранее формул, получим

,

где, как и раньше

.

Тогда искомое приращение водоизмещения

.

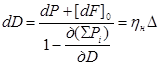где 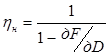– коэффициент Нормана, являющийся частным случаем обобщенного коэффициента приращения водоизмещения. Нахождение коэффициента Нормана, при наличии подходящего прототипа, не вызывает затруднений.

Связь коэффициентов ηн и ηг

Коэффициенты ηн и ηг можно рассматривать как величины, характеризующие нагрузку судна. Преобразуем алгебраическое уравнение масс. Если исключить из рассмотрения массу экипажа, то независимые массы будут представлены только массой перевозимого груза, которую можно выразить через соответствующий коэффициент утилизации водоизмещения.

D = ΣPi(D) + P = ΣPi(D) + Pг = ΣPi(D) + ηгD.

Из полученной зависимости следует, что

.

Найдем частную производную переменных масс по водоизмещению.

.

Тогда коэффициент Нормана

.

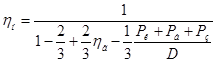После приведения подобных получим,

.

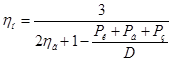В полученной формуле четко прослеживается влияние ηг на ηн. Если же предположить, что степень при D в зависимостях для масс всех разделов равна единице, то выражение упрощается до вида

.

Эта простая зависимость будет давать несколько преувеличенное значение ηн при том же значении ηг.

Графическая интерпретация дифференциальных уравнений масс

Пусть алгебраическое уравнение масс судна-прототипа выражается функцией D0 = ΣРi(D) + Р0 и имеет решение соответствующее точке А0 (рис. 7). Для проектируемого судна функция D = ΣРi(D) + Р решение будет соответствовать точке А. Точки А0 и А будут расположены на пересечении указанных кривых и прямой проходящей под углом 45о к оси абсцисс.

 Скачать реферат

Страница:  1  2  3  4  5  6  7  8  9  10  11  12  13  14  15 
 16  17  18  19 

Другие рефераты на тему «Транспорт»:

• Анализ хозяйственной деятельности предприятий транспорта
• Разработка системы координированного регулирования
• Железнодорожные и воздушные перевозки
• Организация перевозки груза на воздушном транспорте
• Пассажирские перевозки