Исследование систем управления деловыми организациями методами теории принятия решений

Примечание:5– самая высокая оценка.

Оценка конкурентной позиции компании и ее конкурентной силы. Этот этап показывает, как расположена компания относительно соперников по главным показателям конкурентного успеха. Анализ конкурентной силы показывает, где компания сильна, а где слаба.

Результаты оценки положения в конкурентной среде фирмы ООО «Томас» показали, что эта фирма имеет серьез

ных конкурентов, которые уже заслужили авторитет и сильные позиции и как со связями с поставщиками и с потребителями. ООО «Томас» имеет недостаточную популярность в окружающей среде, из-за этого, хотя и качество услуг отличное, спрос на оказание услуг реставрации очень мал. Из-за постоянных сбоев в связях с поставщиками фирма терпит некоторую финансовую затрудненность, поэтому приходится повышать цены на оказываемые услуги, а также нет возможностей расширить ассортимент услуг, иначе фирма в скором будущем потерпит банкротство.

1.6.5 Прогноз развития фирмы

Для успешного функционирования фирмы в ближайшее время большое значение будут иметь следующие факторы:

- предоставление фирме долгосрочного кредита;

- уменьшение доли рынка ремонтных услуг, оказываемых частными лицами;

- рост благосостояния потенциальных клиентов;

- увеличение спроса населения на ремонтные услуги;

- неактивное продвижение фирмами-конкурентами своих услуг.

Поэтому хотя фирма ООО «Томас» и имеет проблемы (неустойчивое финансовое положение, сбои с поставщиками, высока стоимость оказываемых услуг, низкая популярность и т.д.) , которые могут помешать фирме стать конкурентноспособной на рынке, все же у предприятия есть и сильные стороны (качество услуг, применение современных технологий),которые при условии разработки эффективной программы могут фирму вывести на более высокий уровень, расширить потребителей, и ,что в конечном итоге приведет к получению прибыли, как основной целью ООО «Томас»

Наиболее благоприятной возможностью внешней среды является отсутствие активности фирм-конкурентов в продвижении своих услуг на рынке. Разработав рекламную кампанию, фирма может занять значительную долю рынка, повысить объем реализации своих услуг и тем самым улучшить свое финансовое положение.

Однако следует учитывать и возможные ответные действия конкурентов. В настоящее время фирма имеет очень мало сведений о существующих и потенциальных конкурентах. Предприятию следует уделять больше внимания исследованию рынка. Также необходимо создавать долгосрочные планы, чтобы эффективно планировать свою деятельность. А также для реализации задуманного необходимо, в связи с финансовыми проблемами, взять долгосрочный кредит.

Глава 2. Решение задач методами теории принятия решений

2.1 Задание 1

№1,вар.5;

Найти графическим методом из условия:

.

При ограничениях:

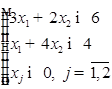
Решение:

Задачи линейного программирования это задачи, в которых требуется найти такие значения переменных X1, X2, …, Xn, при которых некоторая линейная функция от этих переменных принимает максимальное или минимальное значение: E = C1X1 + C2X2 + … + CnXn → max / min при выполнении ограничений на переменные X1, X2, …, Xn, заданных линейными уравнениями или неравенствами:

Здесь p – количество ограничений, имеющих вид «не меньше», q – количество ограничений «равно», m – общее количество ограничений.

Графический метод довольно прост и нагляден для решения задач линейного программирования с двумя переменными. Он основан на геометрическом представлении допустимых решений и целевой функции задачи. Графический метод решения задач линейного программирования применяется для решения задач, в которых имеются только две переменные. Для таких задач имеется возможность графически изобразить область допустимых решений (ОДР).

Как отмечено выше, ОДР – это множество значений переменных X1, X2, …, Xn, удовлетворяющих ограничениям Таким образом, для задач с двумя переменными ОДР представляет собой множество точек (X1; X2), т.е. некоторую область на плоскости (обычно многоугольник). Для задач с тремя переменными ОДР представляет собой многогранник в пространстве, для задач с большим количеством переменных – некоторую область многомерного пространства. Можно доказать, что экстремум (минимум или максимум) целевой функции всегда достигается при значениях переменных X1, X2, …, Xn, соответствующих одной из угловых точек ОДР. Другими словами, оптимальное решение всегда находится в угловой точке ОДР. Поэтому задачу линейного программирования с двумя переменными можно решить следующим образом: построить ОДР на плоскости в системе координат (X1; X2), определить все угловые точки ОДР, вычислить значения целевой функции в этих точках и выбрать оптимальное решение.

Для начала надо построить систему координат. Размерность системы координат определяется количеством переменных в системе неравенств ограничений. Таким образом графическим методом решения обычно пользуются при двух переменных (двумерная система координат), реже при 3-х (трехмерная система координат). При больших количествах переменных не представляется возможным построить многомерную систему координат.

Построение графика области допустимых решений

Необходимо построить прямые ограничивающие область допустимых решений. Каждая прямая соответствует одному неравенству системы неравенств ограничений. Для получения координат двух точек по которым строится прямая знаки неравенств заменяют на равенства и находят корень полученного уравнения относительно каждой переменной. Таким образом получаются точки пересечения прямой с осями координат. Построив прямую определяют область допустимых решений ограничивающуюся этой прямой путем исследования точек находящихся по обе стороны прямой на удовлетворение их координат соответствующему этой прямой неравенству. Так получается область допустимых решений ограниченная прямыми.

Построим область допустимых решений системы ограничений, для чего вычислим координаты точек пересечения этих прямых с осями координат.

(1)

(2)

(3)

(4)

Прямая (1) – проходит через точки (0;3) и (2;0), прямая (2) проходит через точки (0;1) и (4;0), прямая (3) совпадает с осью , прямая (4) совпадает с осью .

 Скачать реферат