Исследование систем управления деловыми организациями методами теории принятия решений

Пересечение всех полуплоскостей, удовлетворяющих ограничениям задачи, представляет собой ОДР, Оптимальное решение находится в одной из угловых точек ОДР (они обозначены как О, A, B, C).

Выбор оптимальной вершины

Оптимальная вершина, т.е вершина границы области допустимых решений, координаты которой соответствуют оптимальному решению задачи, вычисляется при помощи вектора целевой функции

. Вектор строится из начала координат, координатами вектора будут коэффициенты при переменных в целевой функции. VI. При поиске минимума ЦФ необходимо передвигать целевую прямую против направления вектора Последняя по ходу движения вершина ОДР будет точкой минимума ЦФ. Координаты выбранной оптимальной вершины будут значениями соответствующих переменных в целевой функции. И при этих значениях будет достигнуто оптимальное решение

Строим вектор C из точки (0;0) в точку (2;3), так как они являются коэффициентами целевой функции . Точка С – это последняя вершина многоугольника допустимых решений ОABC, через которую проходит целевая прямая, двигаясь против направления вектора С . Поэтому С – это точка минимума ЦФ. Определим координаты точки С из системы уравнений прямых ограничений (1) и (4):

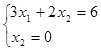(1)

(4)

Получили точку С(2;0). То есть Xопт=(2;0).

Минимальное значение ЦФ

Ответ: оптимальным решением задачи линейного программирования с помощью графического способа является

2.2 Задача 2

Задача 2. Вариант № 5.

Решить транспортную задачу, заданную таблицей:

Теоретические положения:

Транспортная задача – одна из распространенных задач линейного программирования. Ее цель – разработка наиболее рациональных путей и способов транспортирования товаров, устранение чрезмерно дальних, встречных, повторных перевозок. Все это сокращает время продвижения товаров, уменьшает затраты предприятий, фирм, связанные с осуществлением процессов снабжения сырьем, материалами, топливом, оборудованием и т.д.

Общий вид транспортной задачи имеет следующий вид:

Смысл элементов таблицы очевиден. Набор чисел xij называется планом перевозок. Если эти числа удовлетворяют всем ограничениям транспортной задачи (т.е. условиям (1)), то план называется допустимым. Если некоторый допустимый план дает минимум цены, то он называется оптимальным.

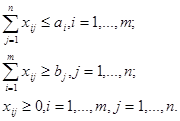(1)

Принято условия (1) переписывать в несколько ином виде. А именно, рассмотрим числа a1, .,am, b1, .,bn; будем считать, что

(2)

если это не так и, скажем,

,

то введем мнимого потребителя с запросом

bn+1=;

если же

,

то введем мнимого поставщика с запасом

am+1=

Для мнимых поставщика и потребителя стоимость перевозок полагается равной нулю. Таким образом, в любом случае можно считать, что таблица из начала этого пункта удовлетворяет условию (1). Кроме того, без потери общности можно считать, что условия (1) являются следующими:

 Скачать реферат