Исследование систем управления деловыми организациями методами теории принятия решений

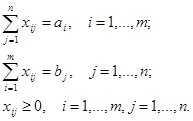(3)

Действительно, если удастся отыскать оптимальный план при условиях (3), то задача будет решена.

Итак, транспортной задачей линейного программирования называется задача поиска минимума функции при ограничениях (3) в предположении, что справедливо условие

(2).

Решение:

1. проверим, является ли данная транспортная задача закрытого типа:

.

Следовательно, данная транспортная задача является закрытой.

2. Найдем исходное опорное решение по методу минимальной стоимости (минимального тарифа). Метод наименьшей стоимости. Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел ai, или bj . Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.

Из всех тарифов Xij отыскиваем наименьший (это Х11=25). Поэтому запасы первого поставщика целиком вывозим первому потребителю, и первый столбец вычеркиваем. Из оставшихся тарифов вновь отыскиваем наименьший – теперь это будет Х12=35. Вывозим оставшийся товар первого поставщика второму потребителю. Вычеркиваем первую строку, т.к. товар поставщика1 закончился. Аналогично заполняем оставшиеся клетки. Нашли следующий опорный план:

Число занятых клеток в таблице = 6.

m+n-1=3+4-1=6,

т.е условие нерожденности выполнено. Получим исходное опроное решение, записанное в виде матрицы:

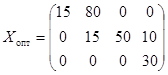
Стоимость перевозки при исходном опорном решении составляет:

3. Проверка решения на оптимальность.

Найденное исходное опорное решение проверяется на оптимальность методом потенциалов по следующему критерию: если опорное решение транспортной задачи является оптимальным, то ему соответствует система m+n действительных чисел Ui и Vj, удовлетворяющих условиям

для занятых клеток, и

- для свободных клеток.

Числа Ui и Vj называют потенциалами. В распределительную таблицу добавляют строку Vj .и столбец Ui. Потенциалы находят из равенства справедливого для занятых клеток. Одному из потенциалов дается произвольное значение, тогда остальные потенциалы определятся однозначно.

Обозначим

,

которую называют оценкой свободных клеток. Если все оценки свободных клеток , то опорное решение является оптимальным. Если хотя бы ода из оценок , то опорное решение не является оптимальным и его можно улучшить, перейдя от одного опорного решения к другому.

Проверим найденное опорное решение на оптимальность, добавив в распределительную таблицу столбец Ui и строку Vj. Теперь дополнительная таблица имеет вид:

 Скачать реферат