Факультативный курс по теме "Элементы комбинаторики" для 8 класса

Рис. 4 Рис. 5 Рис. 6 Рис. 7

При решении комбинаторных задач в некоторых случаях у школьников могут возникать затруднения в различении составляемых соединений, связанных с тем, что для определения их неразличимости нужно выполнить определенные геометрические преобразования.

Составление комбинатор

ных соединений происходит с опорой на запись. Следовательно, в задачах, в которых элементы являются реальными предметами, стоит проблема их обозначения. И если в начале обучения используются конкретные, наглядные заместители реальных предметов, то в дальнейшем учащиеся постепенно переходят к применению условных обозначений. Например, задача: «На каждом флажке должны быть три горизонтальные полоски: красного, синего и белого цвета. Сколько можно получить различных флажков, если менять порядок расположения цветов?» Решая ее, можно выбрать различные способы обозначения флажков.

Непосредственный перебор всех возможных вариантов при решении комбинаторных задач в некоторых случаях может быть затруднен. Облегчить процесс нахождения этих вариантов можно, научив детей пользоваться такими средствами перебора, как таблицы и графы. Они позволяют расчленить ход рассуждений, четко провести перебор, не упустив каких-либо имеющихся возможностей. Решение задач с использованием таблиц и графов является основным содержанием третьего этапа, выделяемого в обучении школьников решению комбинаторных задач.

Сначала как с наиболее простым средством организации перебора учащиеся знакомятся с таблицами. Рассматривая таблицу (рис. 9) ученики открывают принцип её составления. Затем им предлагают заполнить другую таблицу. Проговариваются разные способы заполнения: по строчкам, по столбцам.

В дальнейшем в целях освоения принципа составления таблиц используются и такие задания:

1. Запиши в нужные клетки таблицы (рис. 10) следующие числа: 57, 75, 44, 47, 55, 77, 47. Какие числа нужно записать в оставшиеся клетки?

2. Проверь, правильно ли заполнена таблица (рис. 11).

Когда школьники научатся составлять таблицы, можно переходить к решению комбинаторных задач с их использованием. Как правило, дети неоправданно много времени тратят на вычерчивание самой таблицы: затрудняются определить нужные размеры, разметить все строчки и столбики.

Для того чтобы помочь детям разметить таблицу, методистами были разработаны специальные трафареты (рис. 12). Опишем, как действуют учащиеся, решая с помощью таблицы задачу: «В одной деревне по сложившейся традиции мужчин называют каким-либо из следующих имен: Иван, Петр, Василий и Михаил. Проживают в этой деревне 15 мужчин. Может ли оказаться так, что в деревне нет мужчин с одинаковым именем, отчеством?» Ученик накладывает на тетрадный лист трафарет. Вписывает через «окошечки» на трафарете в верхнюю строчку и в первый столбик данные задачи. Через прорези намечает места записи составляемых объектов. Убирает трафарет. Цветными линиями отчерчивает данные задачи (рис. 13).

Затем ученик заполняет таблицу (рис. 14), подсчитывает число всех возможных отличающихся имен-отчеств, сравнивает с числом мужчин в деревне и отвечает на вопрос задачи.

При заполнении таблиц нужно каждый раз определять, следует записывать составляемое

Рис. 16

Составляются недостающие рукопожатия (эти линии лучше проводить другим цветом, так как потом легче будет подсчитывать общее число рукопожатий). И так действуют до тех пор, пока все не поздороваются друг с другом. По получившемуся графу (рис. 16) подсчитывается число рукопожатий (их всего 10).

Следующая задача: «Сколько двузначных чисел можно составить, используя цифры 1, 2, 3, 4?» приводит учащихся к изображению ориентированного графа (рис. 17). Идея проведения стрелок возникает, когда учащиеся задумываются

Рис. 17

как обозначить, например, число 12: показать, что оно начинается с цифры 1, а оканчивается цифрой 2. петля появляется при обозначении, например, числа 11: стрелка должна начинаться и заканчиваться на одной и той же цифре. Открыв для себя на первых задачах эти условные обозначения (точки, линии, стрелки, петли), учащиеся в дальнейшем применяют их при решении различных задач, составляя графы того или иного вида. Приведем некоторые примеры.

В финал турнира по шашкам вышли два российских игрока,

Рис. 18

два немецких и два американских. Сколько партий будет в финале, если каждый играет с каждым по одному разу и представители одной страны между собой не играют? (граф на рис. 18)

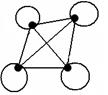
Рис. 19

В зале лежали конфеты четырех сортов. Каждый ребенок взял по 2 конфеты. И у всех оказались отличающиеся наборы конфет. Сколько могло быть детей? (граф на рис. 19)

Сколько разностей можно составить из чисел 30, 25, 17, 9, если для их составления брать по 2 числа? Будут ли среди них разности, значения которых равны? (граф на рис. 20)

Можно предлагать учащимся и обратные задания: составить задачу по имеющемуся графу. Например: «Рассмотри внимательно граф (на рис. 21) и пофантазируй, о какой ситуации он может тебе рассказать». Ученики, рассуждая, что точки могут обозначать людей, предметы, а линии говорят о том, что из них образуются пары, составляют разные варианты задач, например

Рис. 20 Рис. 21

Четыре подружки вечером по телефону созваниваются друг с другом. Сколько звонков было сделано, если каждая подружка поговорила с каждой по одному разу?

В магазине продаются елочные шары четырех видов. Сколько отличающихся наборов, состоящих из двух разных шаров, можно с, состоящих из двух разных шаров, можно составить?