Составление и решение уравнений линейной регрессии

Уравнение имеет вид: У=1,11+0,0161х. Перейдем к исходным переменным х и у, выполнив потенцирование уравнения:

ỹ =101,11(10 0,0161)х, ỹ =12,99*1,038х – уравнение показательной кривой.

Графики построенных уравнений регрессии приведены на рис. 4.

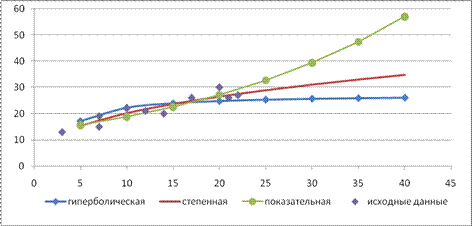
Рисунок 4

9. Коэффициент детерминац

ии: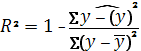

Для сравнения и выбора лучшей модели строим сводную таблицу результатов (табл. 6).

Таблица 6

Вывод: на основании полученных данных лучшей является степенная модель регрессии, т. к. она имеет наибольший коэффициент детерминации R2=0,862, т.е. вариация факторного признака У (объем выпуска продукции) на 86,2% объясняется вариацией фактора Х (объемом капиталовложений), и наименьшую относительную ошибку (в среднем расчетные значения для степенной модели отличаются от фактических данных на 0,034%). Также степенная модель имеет наибольший коэффициент эластичности, т.е. при изменении фактора на 1% зависимая переменная изменится на 0,24%, таким образом степенную модель можно взять в качестве лучшей для построения прогноза.

Задача 2а и 2б

Имеются два варианта структурной формы модели, заданные в виде матриц коэффициентов модели. Необходимо для каждой матрицы записать системы одновременных уравнений и проверить их на идентифицируемость.

Задача 2а

Решение.

Запишем систему одновременных уравнений:

у1= b12 у2+ b13 у3+ a12 х2+ a13 х3

у2= b23 у3+ a21 х1+ a22 х2+ a24 x4

у3 = b32 у2+ a31 х1+ a32х2+a33х3

Проверим каждое уравнение на выполнение необходимого и достаточного условия идентификации.

1) В первом уравнении три эндогенные переменные у1, у2, у3 (Н=3). В нем отсутствуют экзогенные переменные х1, х4 (D=2). Необходимое условие идентификации D+1=H, 2+1=3 выполнено.

Для проверки на достаточное условие составим матрицу из коэффициентов при переменных х1 и х4 (табл. 7)

Таблица 7

Определитель матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, первое уравнение идентифицируемо.

2) Во втором уравнении две эндогенные переменные у2, у3 (Н=2). В нем отсутствует экзогенная переменная х3 (D=1). Необходимое условие идентификации D+1=H, 1+1=2 выполнено.

Для проверки на достаточное условие составим матрицу из коэффициентов при переменных у1 и х3 (табл. 8)

Таблица 8

Определитель матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, второе уравнение идентифицируемо.

3) В третьем уравнении две эндогенные переменные у2, у3 (Н=2). В нем отсутствует экзогенная переменная х4 (D=1). Необходимое условие идентификации D+1=H, 1+1=2 выполнено.

Для проверки на достаточное условие составим матрицу из коэффициентов при переменных у1 и х4 (табл. 9)

Таблица 9

Определитель матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное условие выполнено, третье уравнение идентифицируемо.

Вывод: все уравнения системы идентифицируемы, систему можно решать.

Задача 2б

Решение

Запишем систему уравнений:

у1=b13у3+a11 х1+a13 х3+a14 х4

у2= b21 у1+b23 у3+a22 х2+a24 х4

у3=b31 у1+a31 х1+a33 х3+a34 х4

Проверим каждое уравнение на выполнение необходимого и достаточного условия идентификации.

1) В первом уравнении две эндогенные переменные у1, у3 (Н=2). В нем отсутствует экзогенная переменная х2 (D=1). Необходимое условие идентификации D+1=H, 1+1=2 выполнено.

Для проверки на достаточное условие составим матрицу из коэффициентов при переменных у2 и х2 (табл. 10)

Таблица 10

 Скачать реферат