Составление и решение уравнений линейной регрессии

;

Уравнение линейной регрессии имеет вид: у=11,78+0,76х

С увеличением объема капиталовложений на 1 млн. руб. объем выпускаемой продукции увеличится в среднем на 76 тыс. руб. Это свидетельствует об эффективности работы предприятия.

2. Вычисленные ос

татки и остаточная сумма квадратов представлены в таблице 1. Дисперсию остатков оценим по формуле:

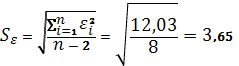– стандартная ошибка оценки. Построим график остатков (рис. 1)

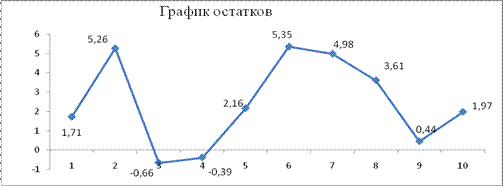
Рисунок 1

3. Проверим выполнение предпосылок МНК на основе анализа остаточной компоненты (см. табл. 1).

Независимость остатков проверяется с помощью критерия Дарбина – Уотсона по формуле , т. к. =0,74, d1=1,08, d2=1,36, т.е. d<d1, значит ряд остатков содержит автокорреляцию.

Для обнаружения гетероскедастичности используем тест Голдфельда – Квандта:

1) Упорядочим наблюдения по мере возрастания переменной х.

2) Разделим совокупность на 2 группы по 5 наблюдений и для каждой определим уравнение регрессии. Воспользуемся инструментом Регрессия пакета Анализ данных, полученные результаты представлены в табл. 2.

Таблица 2

3) Определим остаточную сумму квадратов для первой и второй регрессии .

4) Вычислим отношение , т. к. Fнабл=0,98, Fкр(α,к1,к2)= Fкр(0,05,5,5) =5,05 (из таблицы критерия Фишера), Fнабл <Fкр, то гетероскедастичность отсутствует, предпосылка о равенстве дисперсий остаточных величии не нарушена.

4. Проверим значимость параметров уравнения регрессии с помощью t‑критерия Стьюдента Расчетные значения t‑критерия Стьюдента для коэффициента уравнения регрессии а1 приведены в четвертом столбце протокола Excel, полученном при использовании инструмента Регрессия (рис. 2).

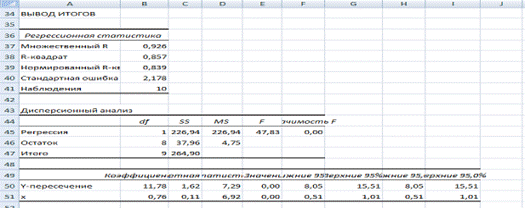
Рисунок 2

Табличное значение t‑критерия Стьюдента 2,30. tрасч=6,92, так как tрасч>tтабл, то коэффициент а1 значим.

5. Значение коэффициента детерминации (R – квадрат) можно найти в таблице Регрессионная статистика (рис. 2). Коэффициент детерминации/ Он показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 85,7% вариации зависимой переменной (объем выпуска продукции) учтено в модели и обусловлено влиянием включенного фактора (объем капиталовложений).

Значение F – критерия Фишера можно найти в таблице протокола Excel (рис. 2), Fрасч=47,83. Табличное значение F – критерия при доверительной вероятности 0,05 равно 4,46, т. к. Fрасч>Fтабл, уравнение регрессии следует признать адекватным.

Определим среднюю относительную ошибку аппроксимации? в среднем расчетные значения у для линейной модели отличаются от фактических на 1% – хорошее качество модели.

6. Осуществим прогнозирование среднего значения показателя при уровне значимости , если прогнозное значения фактора Х составит 80% от его максимального значения.

 Скачать реферат