Математические задачи исследования операций, которые основаны на нелинейном программировании

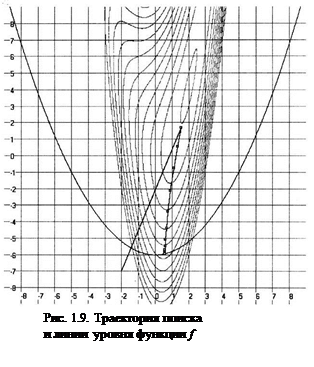
Пример 4: Алгоритмом штрафных функций решить задачу

Этот пример показан на рис. 1.9. Поиск проводится из начальной точки (–2;–7) с параметрами a0=0,1 и b=2.

Здесь, ка

к и в предыдущем примере, на первой итерации алгоритма движение направлено в сторону безусловного минимума целевой функции. Это объясняется небольшим начальным значением параметра штрафа, при котором основное влияние на направление оказывает целевая функция. С возрастанием a направление поиска ориентируется на условный экстремум.

Пример 5: Алгоритмом штрафных функций решить задачу

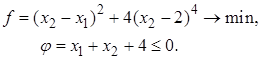
Этот пример приведен на рис. 1.10. Поиск производился при a0=1 и b=10. Такие параметры обусловили другой характер движения к условному минимуму: первая итерация уже не приводит в окрестность безусловного экстремума и траектория не имеет резких изменений направ­ления поиска.

Таким образом, выбор параметров поиска имеет существенное влияние на эффективность алгоритма.

5. Метод барьерных функций

В отличие от метода штрафных функций, данный метод применим к задачам с ограничениями только в виде неравенств.

Исходная задача на условный экстремум задается в виде

f(x) → min; (1.25)

ji(x) £ 0, . (1.26)

Она преобразуется в задачу безусловной минимизации вспомогательной функции

Q(x) = f(x) + mB(x),

где B(x) – барьерная функция, m – параметр барьера.

Обязательное условие: внутренность области не должна быть пустой (имеются точки, в которых "ji (x) < 0).

Барьерная функция строится так, чтобы она была неотрицательной и непрерывной на допустимом множестве и стремилась к бесконечности при приближении изнутри к границе:

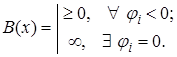
Как и в случае штрафной функции, существует несколько конструкций B(x), удовлетворяющих этим условиям. Но в основном используется барьерная функция в виде

(1.27)

Понятно, что решение вспомогательной задачи зависит от значения параметра барьера. Покажем влияние m на результат минимизации Q.

Примеры

Пример 1: f(x) = x → min; j(x)=3 – x £ 0.

Барьерную функцию строим согласно (1.27). Тогда вспомогательная функция имеет вид 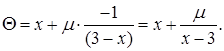Находим точку минимума Q: Отсюда

Следовательно, с уменьшением m точки минимума вспомогательной функции приближаются к минимуму исходной задачи. Геометрическая иллюстрация решения приведена на рис. 1.11.

Как хорошо видно на рис. 1.11, при оптимуме исходной задачи на границе допустимого множества последовательность точек минимума Q с уменьшением m приближается к оптимальному решению изнутри допустимой области. По этой причине метод барьеров называют методом внутренних штрафов.

В связи с возможными трудностями поиска при малых значениях m решается не одна, а последовательность вспомогательных задач с уменьшающимися значениями параметра барьера.

Алгоритм.

1. Выбрать начальную точку x0 так, чтобы "ji(x0)<0; задать точность e, начальное значение m0 и число b Î (0, 1).

2. Минимизировать Q(x) одним из методов безусловной оптимизации, в результате чего определяется .

3. Проверить: если , то остановиться, приняв за оптимальное решение задачи.

4. Положить , за начальную точку принять и вернуться к шагу 2.

Значение m0 можно брать из интервала [2, 10]. Важное замечание касается пункта 2 алгоритма: в процессе поиска минимума вблизи границы из-за дискретности шагов возможен выход за допустимую область, где барьерная функция становится отрицательной, что повлечет расхождение поиска. Поэтому необходима явная проверка на допустимость точек на каждом шаге при минимизации Q.

Пример 2: f(x) = (x1–2)4+( x1–2x2)2® min; j(x)=x2£ 0.

Решение находим, используя вспомогательную функцию

Q=(x1–2)4+(x1–2 x2)2 –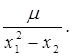

За начальную точку возьмем допустимую точку (0;1), значения m и b принимаем равными 10. Результаты поиска алгоритмом барьерных функций представлены в табл. 1.2 и на рис. 1.12.

Таблица 1.2

Результаты поиска алгоритмом барьерных функций

 Скачать реферат