Математические задачи исследования операций, которые основаны на нелинейном программировании

Необходимо с использованием программы Maxima определить доли капитала, потраченные на покупку каждого вида ценных бумаг при:

а) минимальном риске и заданной эффективности;

б) максимальной эффективности и заданном риске;

в) рискованно-эффективной модели.

◄ Введем обозначения: матрица X={x1, x2 ,…, x6} – доли капитала, потраченные на покупку каждого вида ценных бумаг; матр

ица A – таблица доходностей ценных бумаг, заданная в условии.

а) при минимальном риске и заданной эффективности модель оптимального портфеля Марковица задается выражением (1.29). В данной модели целевая функция r нелинейна, а ограничения линейные функции.

Для вычисления в Maxima необходимо принятые обозначения ввести в программу:

(%i1) X: matrix([x1, x2, x3, x4, x5, x6])$

(%i2) A: matrix([11.293, 11.493, 13.753, 12.936, 12.881, 13.820],

[12.112, 12.919, 12.415, 14.048, 14.770, 14.310],

[11.429, 13.098, 14.277, 14.551, 11.639, 13.524],

[10.526, 11.988, 11.705, 12.466, 11.825, 10.864],

[11.467, 13.364, 12.171, 11.631, 11.923, 13.764],

[11.467, 13.334, 12.338, 14.208, 12.271, 13.324])$

Знак $ используем для того, чтобы не загромождать рабочий лист ненужным отображением обозначений и исходных данных.

Целевая функция в выражении (1.29) есть не что иное как квадратичная форма, которая в матричной форме запишется как , где X – матрица-столбец переменных, а XT– матрица-строка переменных, которую получим при помощи функции transpose. Матрицу ковариаций доходностей ценных бумаг найдем с помощью функции cov, перед применением которой необходимо обязательно загрузить пакеты descriptive и numericalio.

Для получения результатов в удобном для просмотра виде нужно задать точность вычислений с помощью опции fpprec:7 (будет показано 7 значащих цифр, вместо 16 по умолчанию).

(%i3) load (descriptive)$

(%i4) load (numericalio)$

(%i5) fpprec: 7$

Теперь целевую функцию можно записать в Maxima как:

(%i6) r: transpose(X).cov (A).X$

Ограничение в матричном виде можно записать как , где – средние значения доходностей матрицы A. Для матрицы используем команду mean(A). Тогда ограничение примет вид в виде X.mean(A).

Поскольку имеется шесть независимых переменных, а в ограничениях имеем еще два уравнения, то для составления линейной системы, в которой число переменных должно быть равно числу уравнений, вводим две дополнительные переменные (множители Лагранжа) g1, g2. Тогда функция Лагранжа будет иметь вид:

,

где , – ограничения в выражении 5.29.

Необходимым условием существования условного экстремума функции является равенство нулю всех частных производных функции Лагранжа:

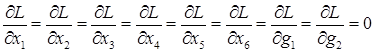
В программе Maxima функцию Лагранжа запишем как:

(%i7) L:r+g1*(X.mean(A)–12)+g2*(x1+x2+x3+x4+x5+x6–1)$

С помощью функции linsolve решим систему из 8-ми уравнений с 8-ми неизвестными:

(%i8) linsolve([diff(L,x1), diff(L,x2), diff(L,x3), diff(L,x4), diff(L,x5), diff(L,x6), diff(L,g1), diff(L,g2)], [x1,x2,x3,x4,x5,x6,g1,g2]), numer;

(%o8) [x1=0.15798, x2=0.62034, x3=0.60815, x4=–0.29938, x5=0.4285,

x6=–0.5156, g1=–0.016695,g2=0.11864]

Решение задачи нам не подходит поскольку инвестор еще не вкладывал деньги в акции, и, следовательно, отрицательные значения переменных невозможны. Для устранения этой проблемы присвоим отрицательным переменным значение равное нулю (x4=x6=0) и заново повторим расчет:

(%i9) linsolve([diff(L,x1), diff(L,x2), diff(L,x3), x4, diff(L,x5), x6, diff(L,g1),

diff(L,g2)], [x1,x2,x3,x4,x5,x6,g1,g2]), numer;

(%o9) [x1=0.53933, x2=0.23621, x3=0.19622, x4=0, x5=0.02824, x6=0,

g1=–0.0077851, g2=–0.27808]

Решение найдено. Сделаем проверку и вычислим минимальный риск портфеля ценных бумаг:

(%i10) x1:0.53933$ x2:0.23621$ x3:0.19622$ x4:0$ x5:0.02824$ x6:0$

(%i16) ev(x1+x2+x3+x4+x5+x6);

(%o16) 1.0

(%i17) ev(r);

(%o17) 0.18575

Таким образом, при минимальном риске и заданной эффективности инвестору следует вложить деньги в следующем соотношении:

· 53,9 % в акции №1;

· 23,6 % в акции №2;

· 19,6 % в акции №3;

· 2,9 % в акции №5.

При этом минимальный риск портфеля .

б) при максимальной эффективности и заданном (приемлемом) риске модель оптимального портфеля Марковица задается выражением 5.30. Однако, поскольку в данной модели целевая функция линейна, а в ограничениях одна из функций нелинейна, то перейдем к двойственной задаче 5.29 с одним изменением – сделаем заданную эффективность переменной величиной (введем дополнительную переменную y). Введение этой переменной позволит рассчитать отклонение эффективности от заданного значения, а затем посчитать и максимальную эффективность .Тогда получим следующую модель задачи:

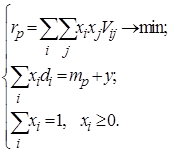
В новом рабочем листе программы Maxima заново введем первые шесть строк из модели минимального риска. Поэтому ввод начнем с ячейки (%i7):

Введем целевую функцию и функцию Лагранжа:

(%i7) L:r+g1*(X.mean(A)–12–y)+g2*(x1+x2+x3+x4+x5+x6–1)$

Решим систему из 8-ми уравнений с 8-ми неизвестными с помощью функции linsolve. Кроме того, используем для упрощения результатов функции ratsimp и float:

(%i8) ratsimp(float(linsolve([diff(L,x1), diff(L,x2), diff(L,x3), diff(L,x4), diff(L,x5), diff(L,x6), diff(L,g1), diff(L,g2)], [x1,x2,x3,x4,x5,x6,g1,g2])));

(%o8) [x1=-(22795378539428444*y-4537670339779197)/28722781234937848,

x2=(2042987868973048*y+3563561400232913)/5744556246987570,

x3=(663161266743035*y+2183481844408430)/3590347654367231,

x4=-(3687740930219273*y+17198034751936498)/57445562469875696,

x5=(8251473140996895*y+12603202586464272)/29412127984576352,

x6=(530470143236891*y-7404674255574559)/14361390617468924,

g1=-(4013841060378303*y+19640954047503052)/1176485119383054336,

g2=(870518148102923*y+4259714641710461)/35903476543672312]

 Скачать реферат