Математические задачи исследования операций, которые основаны на нелинейном программировании

Математическое ожидание доходности портфеля обозначим через :

.

Дисперсию доходности портфеля обозначим через :

.

Назовем – эффективностью портфеля, а величину – риском портфеля.

Каждый владелец портфеля ценных бумаг сталкивается с дилеммой: хочется иметь эффективность больше, а риск меньше. Однако поскольку «нельзя поймать двух зайцев сразу», необходимо сделать определенный выбор между эффективностью и риском. Этот выбор, в конечном счете, определяется отношением лица принимающего решение (ЛПР) к эффективности и риску.

Модель оптимального портфеля Марковица, которая обеспечивает минимальный риск и заданную эффективность имеет вид:

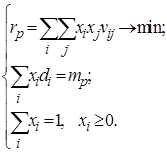(1.29)

Оптимальный портфель Марковица максимальной эффективности и заданного (приемлемого) риска можно представить в виде:

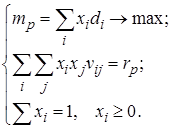(1.30)

Необходимо определить доли капитала, потраченные на покупку каждого вида ценных бумаг: x1, x2 ,…, xn.

Исходными данными для расчета является табл. 1.3.

Таблица 1.3

Таблица доходностей ценных бумаг

Для вычисления используются нижеследующие расчетные формулы.

Среднее арифметическое доходности i-ой ценной бумаги:

(1.31)

Ковариация или корреляционный момент доходностей ценных бумаг:

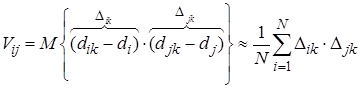, (1.32)

где и – отклонения доходностей i-ой и j-ой бумаг от средней арифметической доходности.

Приведенные модели Марковица в ограничениях используются заранее определенные уровни риска и доходности. Эти модели зависят от знаний и мнений экспертов рынка ценных бумаг и не дают игроку рынка ответ на самый главный вопрос, в какую же игру играть – рискованную (прибыльную) или нерискованную (мало-доходную). Для преодоления этого противоречия была предложена рискованно-прибыльная модель, которая позволяет не рассуждать над проблемой определения допустимого уровня риска для каждого портфеля, и имеет вид:

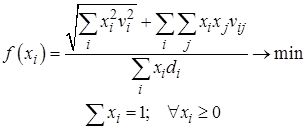, (1.33)

где – вариация прибыльности ценных бумаг i-го вида, – ковариация прибыльности ценных бумаг i-го и j-го видов.

Работоспособность предложенной сверстки обоих критериев доказана путем числовых экспериментов методом «Монте-Карло» [5].

Рассмотренные модели относятся к моделям нелинейного программирования. Для их решения используется метод Лагранжа и программа Maxima.

Пример

Задана эффективность портфеля ценных бумаг и риск портфеля . Ценные бумаги заданы табл. 1.4.

Таблица 1.4

Таблица доходностей ценных бумаг

 Скачать реферат