Математические задачи исследования операций, которые основаны на нелинейном программировании

Очевидно, что при смешанных и нелинейных ограничениях алгоритм весьма существенно усложняется и требует большого объема вычислений. Поэтому метод проектирования градиентов целесообразно применять при линейных ограничениях.

4. Метод штрафных функций

Совершенно иной подход используется в методах штрафных и барьерных функций. Ограничения задачи специальным образом

отражаются в критерии, в результате чего критерий модифицируется, а исходная задача на условный экстремум сводится к задаче на безусловный экстремум.

В методе штрафных функций в критерий вводится штраф при нарушении условий задачи. Пусть в общем случае имеем задачу

f(x) → min; (1.20)

ji(x) £ 0, ; (1.21)

yi(x) = 0 , . (1.22)

Тогда можно построить вспомогательную функцию

Q(x) = f(x) + a×H(x), (1.23)

где H(x)–функция штрафа, a – параметр штрафа.

Вспомогательная функция играет роль модифицированного критерия, который при выполнении всех ограничений должен совпадать с исходным. Поэтому необходимо, чтобы в допустимой области Н(x) равнялась нулю, а вне ее была положительной. Для задачи (1.20)–(1.22) функция штрафа включает две составляющие , учитывающие ограничения-неравенства и ограничения-равенства соответственно и удовлетворяющие условиям

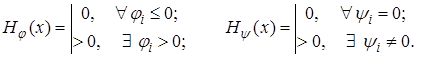(1.24)

Возможны разные конструкции функций, обладающих указанными свойствами. Типичные представители составляющих штрафной функции имеют вид

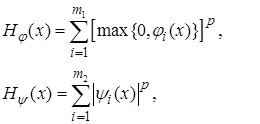
где р – натуральное число. Для дифференцируемости функций берут четные значения р, обычно р = 2. Чем больше a, тем сильнее влияет функция штрафа и, значит, тем точнее выполняются условия задачи.

Примеры

Пример 1: f(x) = x → min; j(x)=3 – x £ 0.

Ответ очевиден: x*=3. Теперь сведем эту задачу к определению безусловного экстремума вспомогательной функции. Построим штрафную функцию в соответствии с (1.24): H = [max (0, 3–x)]2. Тогда приходим к задаче Q=x+a[max (0, 3-x)]2® min.

На рис. 1.6 и 5.6 показаны соответственно функции aH и Q для двух значений a. Видно, что точки минимума вспомогательной функции с увеличением a приближаются к точке условного минимума исходной задачи. Такой же вывод следует из аналитического решения. Действительно, при x<3 вспомогательная функция имеет вид:

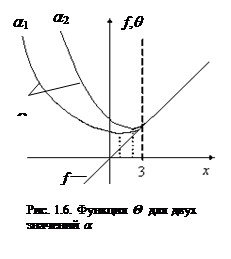
Находим минимум этой функции:

Отсюда получаем

Пример 2: Рассмотрим влияние параметра шага в задаче

Здесь и

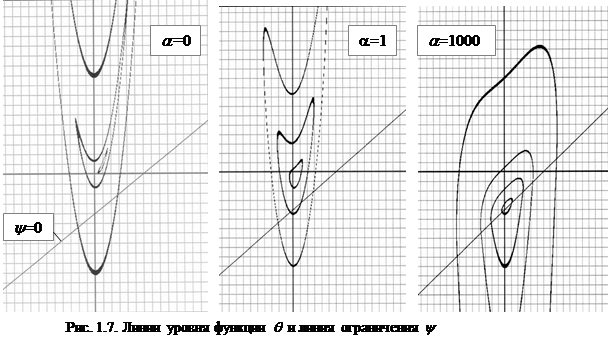
На рис. 1.7 построены линии уровня функции q для разных значений a и линия ограничения y.

При a=0 имеем q=f, и минимум q достигается в точке безусловного минимума f: x1=x2=1. С увеличением a меняется форма линий уровня q и положение минимума. При a=1 минимум q смещается к линии ограничения, а при a=1000 он практически точно совпадает с условным минимумом задачи.

В обоих примерах с увеличением a генерируемые точки приближаются к оптимальному решению извне допустимого множества. Поэтому ряд авторов называют рассматриваемый метод методом внешних штрафов.

Таким образом, чтобы безусловный минимум вспомогательной функции был близок к условному минимуму, необходимо брать очень большое значение a. Однако при больших a возникают серьезные трудности при поиске минимума вспомогательной функции. Поэтому предлагается решать последовательность задач минимизации Q с возрастающими значениями a. При этом в качестве начальной точки следующей задачи берется оптимальная точка предыдущей. Такой прием использован в следующем алгоритме штрафных функций.

Алгоритм.

1. Задать: начальную точку x0, точность e, начальное значение a0 и число b >1.

2. Минимизировать Q(x) одним из методов безусловной оптимизации, в результате чего определяется .

3. Проверить: если , то остановиться, приняв за оптимальное решение задачи.

4. Положить , за начальную точку принять и вернуться на шаг 2.

Рекомендуется выбирать значения параметров алгоритма из диапазонов: a0Î(0,1], bÎ(1,10]. Начальную точку следует задавать в недопустимой области.

Пример 3: Алгоритмом штрафных функций решить задачу

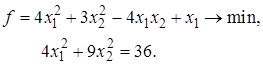
Возьмем начальную точку x0=(–5;5), a0=0,21, b=5 и e=0,0001. Применяя для минимизации Q метод Ньютона, получаем результаты, представленные в табл. 1.1.

Как следует из табл. 1.1, решение с заданной высокой точностью получено за 11 итераций алгоритма. Заметим, что несмотря на увеличение a значение aH сходится к нулю, обеспечивая сходимость алго­ритма.

Траектория поиска и линии уровня функции f изображены на рис. 1.8.

Таблица 1.1 Минимизация функции Q методом Ньютона

 Скачать реферат