Разработка системы учета и прогнозирования ежедневных поступлений страховых взносов на обязательное пенсионное страхование

Коэффициент корреляции является мерой линейной связи между зависимыми случайными величинами: он показывает, насколько хорошо в среднем может быть представлена одна из величин в виде линейной функции от другой.

Коэффициент корреляции вычисляется по формуле:

Формула 5

,

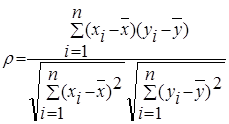где ,и ¾ среднее арифметическое значение соответственно по x и y.

Коэффициент корреляции между случайными величинами по абсолютной величине не превосходит 1. Чем ближе к 1, тем теснее линейная связь между x и y.

В случае нелинейной корреляционной связи условные средние значения располагаются около кривой линии. В этом случае в качестве характеристики силы связи рекомендуется использовать корреляционное отношение, интерпретация которого не зависит от вида исследуемой зависимости.

Корреляционное отношение вычисляется по формуле:

Формула 6

,

где , а числитель характеризует рассеяние условных средних около безусловного среднего .

Всегда . Равенство соответствует некоррелированным случайным величинам; тогда и только тогда, когда имеется точная функциональная связь между y и x. В случае линейной зависимости y от x корреляционное отношение совпадает с квадратом коэффициента корреляции. Величина используется в качестве индикатора отклонения регрессии от линейной.

Корреляционное отношение является мерой корреляционной связи y с x в какой угодно форме, но не может дать представления о степени приближенности эмпирических данных к специальной форме. Чтобы выяснить насколько точно построенная кривая отражает эмпирические данные вводится еще одна характеристика ¾ коэффициент детерминированности.

Для его описания рассмотрим следующие величины. - полная сумма квадратов, где среднее значение .

Можно доказать следующее равенство

Формула 7

.

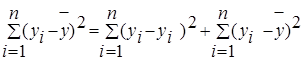Первое слагаемое равно 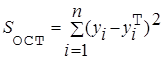и называется остаточной суммой квадратов. Оно характеризует отклонение экспериментальных данных от теоретических.

Второе слагаемое равно и называется регрессионной суммой квадратов и оно характеризует разброс данных.

Очевидно, что справедливо следующее равенство

.

Коэффициент детерминированности определяется по формуле:

Формула 8

Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминированности , который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями y. В противоположном случае, если коэффициент детерминированности равен 0, то уравнение регрессии неудачно для предсказания значений y.

Коэффициент детерминированности всегда не превосходит корреляционное отношение. В случае когда выполняется равенство то можно считать, что построенная эмпирическая формула наиболее точно отражает эмпирические данные.

1.3.2 Анализ методики расчета параметров уравнения аппроксимации

Имеются данные о поступлении платежей на страховую и накопительную части трудовой пенсии в апреле 2008-2009 гг. Требуется подобрать наилучшее аппроксимирующее уравнение для прогнозирования подневных доходов на 2010 год.

Таблица 1.2 - Данные о ежедневных платежах за март 2008-2009 гг.

 Скачать реферат