Разработка системы учета и прогнозирования ежедневных поступлений страховых взносов на обязательное пенсионное страхование

где

у – ежедневные платежи марта 2009 года;

х – ежедневные платежи марта 2008 года.

Шаг 2

Аппроксимируем функцию линейной функцией . Для определения коэффициентов и 1 src="images/referats/9780/image031.png">воспользуемся системой

Система 4

Используя итоговые суммы таблицы 3, расположенные в ячейках B24, C24, D24, E24, запишем систему в виде

Система 5

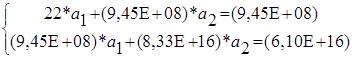
решив которую, получаем: а1 = 22415273,4 и а2 = 0,478067637. Решение системы производили средствами MS Excel. Результаты представлены в таблице 4

Таблица 1.4 - Решение системы уравнений в MS Excel

В таблице 4 в ячейках А4:В5 записана формула {=МОБР(A1:B2)}.

В ячейках C4:C5 записана формула {=МУМНОЖ(A4:B5;C1:C2)}.

Шаг 3

Далее аппроксимируем функцию квадратичной функцией . Для определения коэффициентов , и воспользуемся системой

Система 6

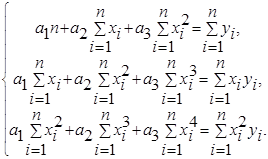
Используя итоговые суммы таблицы 3, расположенные в ячейках B24, C24, D24, E24, F24, G24, H24, запишем систему в виде

Система 7

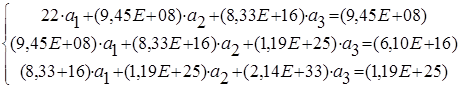
решив которую, получаем а1 = 114949314, а2 = -3,46784603, а3 = 2,0307E-08.

Таким образом, квадратичная аппроксимация имеет вид

у = 114949314 - 3,46784603*х + 2,0307E-08*х2

Решение системы производили средствами MS Excel. Результаты представлены в таблице 5.

Таблица 1.5 - Решение системы уравнений в случае квадратичной аппроксимации

Шаг 4

Теперь аппроксимируем функцию экспоненциальной функцией . Для определения коэффициентов и прологарифмируем значения и используя итоговые суммы таблицы 3, расположенные в ячейках B24, D24, I24, J24 получим систему

Система 8

где .

Решив систему, найдем с = 16,45413618, а2 = 1,71028E-08.

После потенцирования получим а1 = 13993957,34.

Таким образом, экспоненциальная аппроксимация имеет вид

.

Решение системы проводили, пользуясь средствами Microsoft Excel. Результаты представлены в таблице 6.

Таблица 1.6 - Решение системы уравнений при экспоненциальной аппроксимации

В ячейках А4:В5 записана формула {=МОБР(А1:В2)}.

В ячейках С4:С5 записана формула {=МУМНОЖ(А4:В5;С1:С2)}.

В ячейке С6 записана формула =EXP(C4).

Вычислим среднее арифметическое значение показателей х и у в таблице 1.7:

Таблица 1.7 - Среднее арифметическое показателей

 Скачать реферат