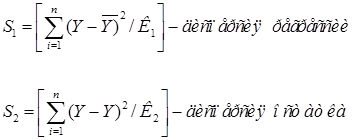Процесс обработки статистикой информации

Проверим значимость коэффициента корреляции, т.е. возможность отвергнуть теорию о некоррелированности рассматриваемых величин.

Для этого определим коэффициент (6)

Для нашего примера

В справочнике найдем табличное значение критерия значимости. При задан

ной вероятности Р=0,95 и N=30 . Условие, при котором отвергают гипотезу о некоррелированности исследуемых величин . Условие выполняется, следовательно гипотезу некоррелированности признаков можно отвергнуть с заданным уровнем надежности.

Построение линейной регрессионной модели.

Наибольшее распространение получил метод наименьших квадратов МНК, при использовании которого ставится требование, чтобы сумма квадратов разностей между эмпирическими и теоретическими значениями была минимальной.

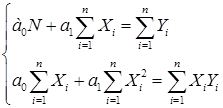
Оценка линейности связи

Для решения поставленной задачи используем дисперсионный анализ. Если теоретическая линейная регрессия действительно выражает форму эмпирической связи, то отклонения эмпирической линии регрессии от теоретической будут случайными.

В случае если в действительности связь не прямолинейна, отклонения не будут случайными, а будут отражать кривизну эмпирической регрессии. Поэтому вопрос о линейной регрессии может быть решен путем сравнения неслучайных и случайных отклонений.

Неслучайные отклонения характеризуются дисперсией отклонения теоретической регрессии от среднего. Случайные отклонения характеризуются дисперсией остатка.

Определение общей дисперсии по результативному признаку

где К1 - число степеней свободы, приходящееся на регрессию; равно числу независимых переменных (для парной регрессии К1=1)

К2-число степеней свободы, приходящееся на остаток (К2=N - К1-1=28)

Y - теоретическое значение результативного признака, найденное по уравнению парной регрессии.

Таблица 9 - Расчет общей дисперсии

 Скачать реферат