Процесс обработки статистикой информации

Проанализировать данные динамического ряда по второму леспромхозу:

1) Исчислить базисным методом абсолютный прирост, коэффициент роста, темп роста, темп прироста и значение одного процента прироста в абсолютном выражении

2) Представить данные динамики объема вывозки древесины за 1976-1985гг. графически

3) Провести выравнивание динамического ряда по способу наименьших квадратов. <

p>Абсолютный прирост - разность между сравниваемым уровнем и уровнем более раннего периода, принятым за базу сравнения. При расчете базисным методом за базу принимают значение одного и того же уровня, например, начального.

∆i=yi - y0, (13)

∆1=172-169=3 (тыс. м3/год)

∆2=183-169=14 (тыс. м3/2года)

∆3=189-169=20 (тыс. м3/3года)

∆4=198-169=29 (тыс. м3/4года)

∆5=212-169=43 (тыс. м3/5лет)

∆6=235-169=66 (тыс. м3/6лет)

∆7=249-169=80 (тыс. м3/7лет)

∆8=268-169=99 (тыс. м3/8лет)

∆9=301-169=132 (тыс. м3/9лет) Коэффициент роста Ki определяется как отношение данного уровня к предыдущему или базисному, показывает относительную скорость изменения ряда. Если коэффициент роста выражается в процентах, то его называют темпом роста.

Темп роста - отношение сравниваемого уровня (боле позднего) к уровню, принятому за базу сравнения (более раннему). Данный показатель говорит о том, сколько процентов составил сравниваемый уровень по отношению к уровню, принятому за базу, или во сколько раз сравниваемый уровень больше уровня, принятого за базу.

Ki/0 = yi/y0, (14)

K1/0=172/169=1,018 (раз) рост 1,8%

K2/0=183/169=1,083 (раз) рост 8,3%

K3/0=189/169=1,118 (раз) рост 11,8%

K4/0=198/169=1,171 (раз) рост 17,1%

K5/0=212/169=1,254 (раз) рост 25,4%

K6/0=235/169=1,391 (раз) рост 39,1%

K7/0=249/169=1,473 (раз) рост 47,3%

K8/0=268/169=1,586 (раз) рост 58,6%

K9/0=301/169=1,781 (раз) рост 78,1%

Темп прироста (относительный прирост) - отношение абсолютного изменения к базисному уровню или

Тпi=Ki*100-100, (15), Тп1=1,018*100-100=1,8 %

Тп2=1,083*100-100=8,3 %

Тп3=1,118*100-100=11,8 %

Тп4=1,171*100-100=17,1 %

Тп5=1,254*100-100=25,4 %

Тп6=1,391*100-100=39,1 %

Тп7=1,473*100-100=47,3 %

Тп8=1,586*100-100=56,8 %

Тп9=1,78*100-100=78,1 %

Абсолютное значение 1% прироста равно сотой части базисного уровня 132/78=1,69 (тыс. м3) или 169/100=1,69 (тыс. м3)

Простейшей системой корреляционной связи является линейная связь между двумя признаками - парная линейная корреляция.

Практическое ее значение в том, что есть системы, в которых среди всех факторов, влияющих на результативный признак, выделяется один важнейший фактор, который в основном определяет вариацию результативного признака. Уравнение парной линейной корреляционной связи называется уравнением парной регрессии

= а + bt, (16)

где - среднее значение результативного признака;

t - порядковый номер периодов или моментов времени;

a - свободный член уравнении;

b - коэффициент регрессии, измеряющий среднее отношение отклонения результативного признака от его средней величины к отклонению факторного признака от его средней величины на одну единицу его измерения.

Параметры уравнения (16) рассчитываются методом наименьших квадратов (МНК). Система нормальных уравнений в данном случае имеет вид:

Исходное условие МНК для прямой линии имеет вид:

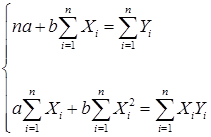
Поиск параметров уравнения можно упростить, если отчет времени производить так, чтобы сумма показателей времени изучаемого ряда динамики была равна нулю (). При четном числе уровней динамического ряда (как в нашем случае) периоды верхнее половины ряда (до середины) нумеруются - 1, - 3, - 5 и т.д., а нижней - +1, +3, +5 и т.д. При этом условии будет равна нулю, и система нормальных уравнений преобразуется следующим образом:

Откуда

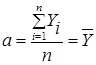= 217,6 и 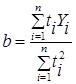= 169,01

Расчет параметров уравнения прямой представлен в таблице 12.

Таблица 12

 Скачать реферат