Моделирование нейронных сетей для прогнозирования стоимости недвижимости

4.2 Функционирование ИНС

Модели НС могут быть программного и аппаратного исполнения. Рассмотрим модель НС программного исполнения.

Несмотря на существенные различия, отдельные типы НС обладают несколькими общими чертами.

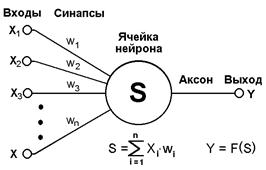
Рисунок 4.4 - Структурная схема искусственного нейрона

Во-первых, основу каждой НС

составляют относительно простые, в большинстве случаев – однотипные, элементы (ячейки), имитирующие работу нейронов мозга. Далее под нейроном будет подразумеваться искусственный нейрон, то есть ячейка НС. Каждый нейрон характеризуется своим текущим состоянием по аналогии с нервными клетками головного мозга, которые могут быть возбуждены или заторможены. Он обладает группой синапсов – однонаправленных входных связей, соединенных с выходами других нейронов, а также имеет аксон – выходную связь данного нейрона, с которой сигнал (возбуждения или торможения) поступает на синапсы следующих нейронов. Общий вид нейрона приведен на рисунке 4.4. Каждый синапс характеризуется величиной синаптической связи или ее весом wi, который по физическому смыслу эквивалентен электрической проводимости.

Текущее состояние нейрона определяется, как взвешенная сумма его входов:

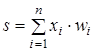.(4.4)

Выход нейрона есть функция его состояния:

(4.5)

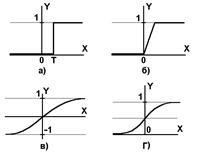
Рисунок 4.5 - а) функция единичного скачка; б) линейный порог (гистерезис); в) сигмоид – гиперболический тангенс; г) сигмоид – формула (3.6)

Нелинейная функция f называется активационной и может иметь различный вид, как показано на рисунке 4.5. Одной из наиболее распространенных является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид (т.е. функция S-образного вида):

.(4.5)

При уменьшении a сигмоид становится более пологим, в пределе при a=0 вырождаясь в горизонтальную линию на уровне 0.5, при увеличении a сигмоид приближается по внешнему виду к функции единичного скачка с порогом T в точке x=0. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0,1]. Одно из ценных свойств сигмовидной функции – простое выражение для ее производной

(4.6)

Следует отметить, что сигмоидная функция дифференцируема на всей оси абсцисс, что используется в некоторых алгоритмах обучения. Кроме того она обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыщение от больших сигналов, так как они соответствуют областям аргументов, где сигмоид имеет пологий наклон.

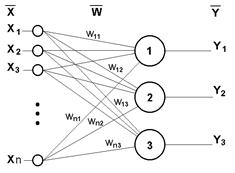
Рисунок 4.6 - Однослойный перцептрон

Возвращаясь к общим чертам, присущим всем НС, отметим, во-вторых, принцип параллельной обработки сигналов, который достигается путем объединения большого числа нейронов в так называемые слои и соединения определенным образом нейронов различных слоев, а также, в некоторых конфигурациях, и нейронов одного слоя между собой, причем обработка взаимодействия всех нейронов ведется послойно.

Выбор структуры НС осуществляется в соответствии с особенностями и сложностью задачи. Для решения некоторых отдельных типов задач уже существуют оптимальные, на сегодняшний день, конфигурации. Если же задача не может быть сведена ни к одному из известных типов, разработчику приходится решать сложную проблему синтеза новой конфигурации. При этом он руководствуется несколькими основополагающими принципами: возможности сети возрастают с увеличением числа ячеек сети, плотности связей между ними и числом выделенных слоев; введение обратных связей наряду с увеличением возможностей сети поднимает вопрос о динамической устойчивости сети; сложность алгоритмов функционирования сети (в том числе, например, введение нескольких типов синапсов – возбуждающих, тормозящих и др.) также способствует усилению мощи НС. Вопрос о необходимых и достаточных свойствах сети для решения того или иного рода задач представляет собой целое направление нейрокомпьютерной науки. Так как проблема синтеза НС сильно зависит от решаемой задачи, дать общие подробные рекомендации затруднительно. В большинстве случаев оптимальный вариант получается на основе интуитивного подбора.

Очевидно, что процесс функционирования НС, то есть сущность действий, которые она способна выполнять, зависит от величин синоптических связей, поэтому, задавшись определенной структурой НС, отвечающей какой-либо задаче, разработчик сети должен найти оптимальные значения всех переменных весовых коэффициентов (некоторые синоптические связи могут быть постоянными).

4.3 Модель многослойного персептрона

Среди искусственных нейронных сетей, применяемых в экономике, наибольшее распространение получили ИНС, обучаемые с учителем, а среди них – многослойные нейронные сети типа МП.

На сегодняшний день многослойный персептрон - одна из самых используемых нейросетей. Одно из главных преимуществ многослойного персептрона, это возможность решать алгоритмически неразрешимые задачи или задачи, для которых алгоритмическое решение неизвестно, но для которых возможно составить репрезентативный набор примеров с известными решениями. При обучении нейросеть, за счёт своего внутреннего строения, выявляет закономерности в связи входных и выходных образов, тем самым как бы "обобщает" полученный на обучающей выборке опыт. В этой способности к обобщению и состоит основа привлекательности многослойного персептрона. Исследователь может сам и не знать какова зависимость между входными и выходными образами, достаточно иметь большой набор векторов, для которых известен ожидаемый выход. Многослойный персептрон можно успешно применять для решения следующих задач:

– прогнозирование поведения рынка;

– распознавание речи;

– анализ изображений;

– экспертные системы и т.д.

4.3.1 Структура МП

Многослойными персептронами называют нейронные сети прямого распространения. В этой ИНС нейроны размещаются последовательными группами, называемыми слоями. Входной сигнал в таких сетях распространяется в прямом направлении, от слоя к слою. Многослойный персептрон в общем представлении состоит из следующих элементов:

– множества входных узлов, которые образуют входной слой;

– одного или нескольких скрытых слоев вычислительных нейронов;

– одного выходного слоя нейронов.

Нейроны в каждом из слоев независимы друг от друга, однако каждый из нейронов связан исходящими связями с каждым нейроном следующего слоя. Таким образом, каждый из нейронов выходного и скрытых слоев принимает входящие сигналы от нейронов предыдущего слоя (рисунок 4.7).

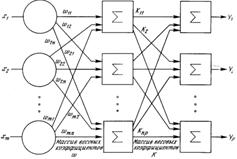
Рисунок 4.7 - Схема многослойной нейронной сети

 Скачать реферат