Моделирование нейронных сетей для прогнозирования стоимости недвижимости

3.2.1 Метод Хольта

Хольт ослабил ограничения метода Брауна, связанные с его однопараметричностью, введением двух параметров сглаживания в его модели прогноза и , на l такт времени в текущий мом

ент t также определяется линейным трендом вида

(3.25)

где обновление прогнозирующих коэффициентов производится по формулам

(3.26)

Таким образом, прогноз по данному методу является функцией прошлых и текущих данных, параметров и , а также начальных значений и .

3.2.2 Метод Хольта-Уинтерса

Уинтерс развил метод Хольта так, чтобы он охватывал еще и сезонные эффекты. Прогноз, сделанный в момент t на l такт времени вперед, равен

(3.27)

где ωτ − коэффициент сезонности, а N − число временных тактов, содержащихся в полном сезонном цикле. Сезонность в этой формуле представлена мультипликативно. Метод использует три параметра сглаживания а его формулы обновления имеют вид

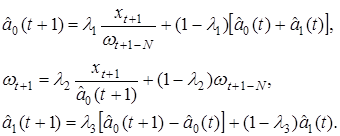(3.28)

Как и в предыдущем случае, прогноз строится на основании прошлых и текущих значений временного ряда, параметров адаптации , и , а также начальных значений и

3.2.3 Аддитивная модель сезонности Тейла−Вейджа

В экономической практике чаще встречаются экспоненциальные тенденции с мультипликативно наложенной сезонностью. Поэтому перед использованием аддитивной модели члены анализируемого временного ряда обычно заменяют их логарифмами, преобразуя экспоненциальную тенденцию в линейную, а мультипликативную сезонность в аддитивную. Преимущество аддитивной модели заключается в относительной простоте ее вычислительной реализации. Рассмотрим модель вида (в предположении, что исходные данные прологарифмированы) где a0(τ) − уровень процесса после элиминирования сезонных колебаний, a1(τ) − аддитивный коэффициент роста, ωt − аддитивный коэффициент сезонности, δt − белый шум.

Прогноз, сделанный в момент t на l временной такт вперед, подсчитывается по формуле

(3.29)

где коэффициенты , и ω вычисляются рекуррентным образом с помощью следующих формул обновления

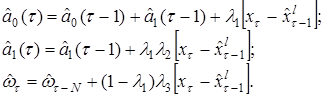(3.30)

В этих соотношениях, как и прежде, N − число временных тактов, содержащихся в полном сезонном цикле, а , и − параметры адаптации.

4. ОСНОВНЫЕ ПОНЯТИЯ НЕЙРОСЕТЕВЫХ ТЕХНОЛОГИЙ

В последние десятилетия в мире бурно развивается новая прикладная область математики, специализирующаяся на искусственных нейронных сетях. Актуальность исследований в этом направлении подтверждается массой различных применений НС. Это автоматизация процессов распознавания образов, адаптивное управление, аппроксимация функционалов, прогнозирование, создание экспертных систем, организация ассоциативной памяти и многие другие приложения. С помощью НС можно, например, предсказывать показатели биржевого рынка, выполнять распознавание оптических или звуковых сигналов, создавать самообучающиеся системы, способные управлять автомашиной при парковке или синтезировать речь по тексту.

Широкий круг задач, решаемый НС, не позволяет в настоящее время создавать универсальные, мощные сети, вынуждая разрабатывать специализированные НС, функционирующие по различным алгоритмам.

4.1 Общие характеристики ИНС

Нейросетевыми технологиями называют комплекс информационных технологий, основанных на применении искусственных нейронных сетей. Искусственные нейронные сети – это программно или аппаратно реализованные системы, построенные по принципу организации и функционирования их биологического аналога – нервной системы человека.

По данным нейробиологии нервная система человека и животных состоит из отдельных клеток – нейронов. Каждая такая клетка выполняет сравнительно простые действия: нейрон способен принимать сигналы от других клеток, и, в свою очередь, передавать сигнал другим клеткам. Исходящий сигнал формируется лишь в случае особой комбинации входящих сигналов. Таким образом, нейрон можно представить как простейший вычислительный элемент: он преобразует входящую информацию в исходящую. Это преобразование происходит в сравнительно короткий срок: время срабатывания нейрона – 2–5 мс.

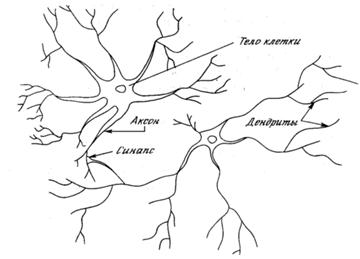
Рисунок 4.1 - Биологический нейрон

На рисунке 4.1 показана структура пары типичных биологических нейронов. Дендриты идут от тела нервной клетки к другим нейронам, где они принимают сигналы в точках соединения, называемых синапсами. Принятые синапсом входные сигналы подводятся к телу нейрона. Здесь они суммируются, причем одни входы стремятся возбудить нейрон, другие - воспрепятствовать его возбуждению. Когда суммарное возбуждение в теле нейрона превышает некоторый порог, нейрон возбуждается, посылая по аксону сигнал другим нейронам. У этой основной функциональной схемы много усложнений и исключений, тем не менее, большинство искусственных нейронных сетей моделируют лишь эти простые свойства.

В основе нейросетевых технологий лежит идея о том, что функционирование биологического нейрона можно промоделировать относительно простыми математическими моделями, а вся глубина и гибкость человеческого мышления и другие важнейшие качества нервной системы определяются не сложностью нейронов, а их большим числом и наличием сложной системы связей между ними. В мозге человека их число достигает 1010 – 1012, причем каждый из них связан с 103 – 104 другими нейронами, что создает исключительно комплексную структуру. Эта структура не является статичной: человек находится в процессе постоянного обучения; на основании поступающей в его мозг информации он приобретает опыт и в результате становится способен решать новые задачи. Накопление опыта выражается в изменении характера и «силе» связей между нейронами.

 Скачать реферат