Моделирование нейронных сетей для прогнозирования стоимости недвижимости

Обучение сети, состоящее в определении этих параметров, может сводиться к одному из следующих вариантов:

1. Задаются центры и отклонения, а вычисляются только веса выходного слоя.

2. Определяются путем самообучения центры и отклонения, а для коррекции весов выходного слоя используется обучение с учителем.

3. Определяются все параметры сети с помощью обучения с учителем.

Первые д

ва варианта применяются в сетях, использующих базисные функции с жестко заданным радиусом (отклонением). Третий же вариант, являясь наиболее сложным и трудоемким в реализации, предполагает использование любых базисных функций.

Таким образом, обучение сети заключается в следующем:

– определяются центры ci;

– выбираются параметры σi;

– вычисляются элементы матрицы весов W.

Рассмотрим методику выбора параметров центров и отклонений σ. Центры ci определяют точки, через которые должна проходить аппроксимируемая функция. Поскольку большая обучающая выборка приводит к затягиванию процесса обучения, в РБ-сетях широко используется кластеризация образов, при которой схожие векторы объединяются в кластеры, представляемые затем в процессе обучения только одним вектором. В настоящее время существует достаточно большое число эффективных алгоритмов кластеризации.

Использование кластеризации отражается на формулах (4.20), (4.21) следующим образом:

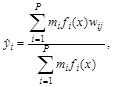(4.22)

где mi - число входных векторов в i-м кластере.

В наиболее простом варианте алгоритм кластеризации, алгоритм k-среднего, направляет каждый образ в кластер, имеющий ближайший к данному образу центр. Если количество центров заранее задано или определено, алгоритм, обрабатывая на каждом такте входной вектор сети, формирует в пространстве входов сети центры кластеров. С ростом числа тактов эти центры сходятся к центрам данных. Кандидатами в центры являются все выходы скрытого слоя, однако в результате работы алгоритма будет сформировано подмножество наиболее существенных выходов.

Как уже указывалось, параметр σi, входящий в формулы для функций преобразования, определяет разброс относительно центра сi. Варьируя параметры ci и σi, пытаются перекрыть все пространство образов, не оставляя пустот. Используя метод k-ближайших соседей, определяют k соседей центра ci и, усредняя, вычисляют среднее значение Величина отклонения от ci служит основанием для выбора параметра σi. На практике часто оправдывает себя выбор

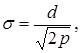(4.23)

где d=max(ci – ck) - максимальное расстояние между выбранными центрами; р - количество нейронов шаблонного слоя (образов).

Если качество аппроксимации является неудовлетворительным, выбор параметров ci и σ, а также определение весов W повторяют до тех пор, пока полученное решение не окажется удовлетворительным.

4.5 Некоторые замечания по выбору сетей

Актуальность тематики прогнозирования продиктована поиском адекватных моделей нейронных сетей, определяемых типом и структурой НС. В ходе исследования установлено, что радиальные базисные сети обладают рядом преимуществ перед сетями типа многослойный персептрон. Во-первых, они моделируют произвольную нелинейную функцию с помощью одного промежуточного слоя. Тем самым отпадает вопрос о числе слоев. Во-вторых, параметры линейной комбинации в выходном слое можно полностью оптимизировать с помощью известных методов моделирования, которые не испытывают трудностей с локальными минимумами, мешающими при обучении МП. Поэтому сеть РБФ обучается очень быстро (на порядок быстрее МП).

С другой стороны, до того как применять линейную оптимизацию в выходном слое сети РБФ, необходимо определить число радиальных элементов, положение их центров и величины отклонений. Для устранения этой проблемы предлагается использовать автоматизированный конструктор сети, который выполняет за пользователя основные эксперименты с сетью.

Другие отличия работы РБФ от МП связаны с различным представлением пространства модели: «групповым» в РБФ и «плоскостным» в МП. Опыт показывает, что для правильного моделирования типичной функции, сеть РБФ требует несколько большего числа элементов. Следовательно, модель, основанная на РБФ, будет работать медленнее и потребует больше памяти, чем соответствующий МП (однако она гораздо быстрее обучается, а в некоторых случаях это важнее).

С «групповым» подходом связано, и неумение сетей РБФ экстраполировать свои выводы за область известных данных. При удалении от обучающего множества значение функции отклика быстро падает до нуля. Напротив, сеть МП выдает более определенные решения при обработке сильно отклоняющихся данных, однако, в целом, склонность МП к некритическому экстраполированию результата считается его слабостью. Сети РБФ более чувствительны к «проклятию размерности» и испытывают значительные трудности, когда число входов велико.

5. МОДЕЛИРОВАНИЕ НЕЙРОННЫХ СЕТЕЙ ДЛЯ ПРОГНОЗИРОВАНИЯ СТОИМОСТИ НЕДВИЖИМОСТИ

5.1 Особенности нейросетевого прогнозирования в задаче оценки стоимости недвижимости

Использование нейронных сетей можно продемонстрировать на примере задачи оценки рыночной стоимости жилой недвижимости. Очевидно, что цена квартиры зависит от многих факторов, например, общей и жилой площади, количества комнат, этажа, территориального расположения дома, его этажности, состояния, наличия коммуникаций и др. Опытные риэлторы справляются с задачей оценки без труда, применяя свои знания и интуицию, опираясь на известные им аналоги и используя ассоциативное мышление. Все эти знания и умения относятся к числу плохо формализуемых, отчасти неосознаваемых, поэтому разработка однозначного алгоритма определения цены на основе значений влияющих факторов – крайне сложная и почти невыполнимая задача.

Вместе с тем, существует значительное число примеров уже оцененных квартир. Используя массив сведений о них, можно попытаться извлечь интересующую зависимость.

Для этого создается нейронная сеть, в которой количество входных нейронов соответствует количеству входных факторов, которые влияют на цену. В выходном слое будет всего один нейрон, соответствующий выходному фактору – цене.

Для обучения необходим массив обучающих примеров. Количество примеров должно быть достаточно большим – по некоторым расчетам, в 10-15 раз больше числа нейронов в сети. Примеры предъявляются ИНС, при этом веса связей внутри нее постепенно изменяются, с тем, чтобы реальный выходной сигнал был как можно ближе к ожидаемому значению выходного фактора. Один цикл предъявления всех учебных образцов называется эпохой. Обычно требуется несколько тысяч эпох, чтобы обучить нейронную сеть, но на современных компьютерах такое обучение занимает несколько минут.

Часть примеров не участвует в обучении, а выделяется в так называемое тестовое множество. На каждой эпохе работа сети проверяется на тестовом множестве. Таким образом тестируется способность ИНС к обобщению: возможности распространить выявленную закономерность к данным, не участвующим в обучении.

 Скачать реферат