Методы решения уравнений линейной регрессии

С помощью программы РЕГРЕССИЯ построим модель по последним четырем наблюдениям (регрессия-2), для этой модели остаточная сумма квадратов .

Рассчитаем статистику критерия:

.

Критическое значение при уровне значимости и числах степеней свободы составляет .

Схема критерия:

Сравним , следовательно, свойство постоянства дисперсии остатков выполняется, модель гомоскедастичная.

2. Для проверки независимости уровней ряда остатков используем критерий Дарбина–Уотсона

.

Предварительно по столбцу остатков с помощью функции СУММКВРАЗН определим ; используем найденную программой РЕГРЕССИЯ сумму квадратов остаточной компоненты .

Таким образом,

Схема критерия:

Полученное значение d=2,375, что свидетельствует об отрицательной корреляции. Перейдем к d’=4-d=1,62 и сравним ее с двумя критическими уровнями d1=0,88 и d2=1,32.

D’=1,62 лежит в интервале от d2=1,32 до 2, следовательно, свойство независимости остаточной компоненты выполняются.

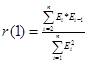
С помощью функции СУММПРОИЗВ найдем для остатков , следовательно r(1)=2,4869Е-14/148,217=1,67788Е-16.

Критическое значение для коэффициента автокорреляции определяется как отношение Ön и составляет для данной задачи

Сравнения показывает, что çr(1)= 1,67788Е-16<0,62, следовательно, ряд остатков некоррелирован.

4) Соответствие ряда остатков нормальному закону распределения проверим с помощью критерия:

.

С помощью функций МАКС и МИН для ряда остатков определим , . Стандартная ошибка модели найдена программой РЕГРЕССИЯ и составляет . Тогда:

Критический интервал определяется по таблице критических границ отношения и при составляет (2,67; 3,57).

Схема критерия:

2,995 (2,67; 3,57), значит, для построенной модели свойство нормального распределения остаточной компоненты выполняется.

Проведенная проверка предпосылок регрессионного анализа показала, что для модели выполняются все условия Гаусса–Маркова.

4. Осуществить проверку значимости параметров уравнения регрессии с помощью t–критерия Стьюдента ().

t–статистика для коэффициентов уравнения приведены в таблице 4.

Для свободного коэффициента определена статистика .

Для коэффициента регрессии определена статистика .

Критическое значение найдено для уравнения значимости и числа степеней свободы с помощью функции СТЬЮДРАСПОБР.

Схема критерия:

Сравнение показывает:

, следовательно, свободный коэффициент a является значимым.

, значит, коэффициент регрессии b является значимым.

5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F–критерия Фишера (), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.

 Скачать реферат