Методы решения уравнений линейной регрессии

Коэффициент детерминации R–квадрат определен программой РЕГРЕССИЯ и составляет .

Таким образом, вариация объема выпуска продукции Y на 79,5% объясняется по полученному уравнению вариацией объема капиталовложений X.

Проверим значимость полученного уравнения с помощью F–критерия Фишера.

F–статистика определена программой

РЕГРЕССИЯ (таблица 2) и составляет .

Критическое значение найдено для уровня значимости и чисел степеней свободы , .

Схема критерия:

Сравнение показывает: ; следовательно, уравнение модели является значимым, его использование целесообразно, зависимая переменная Y достаточно хорошо описывается включенной в модель факторной переменной Х.

Для вычисления средней относительной ошибки аппроксимации рассчитаем дополнительный столбец относительных погрешностей, которые вычислим по формуле

с помощью функции ABS (таблица 5).

По столбцу относительных погрешностей найдем среднее значение (функция СРЗНАЧ).

Схема проверки:

Сравним: 9,31% < 15%, следовательно, модель является точной.

Вывод: на основании проверки предпосылок МНК, критериев Стьюдента и Фишера и величины коэффициента детерминации модель можно считать полностью адекватной. Дальнейшее использование такой модели для прогнозирования в реальных условиях целесообразно.

6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости , если прогнозное значение фактора X составит 80% от его максимального значения.

Согласно условию задачи прогнозное значение факторной переменной Х составит 80% от 49, следовательно, . Рассчитаем по уравнению модели прогнозное значение показателя У:

.

Таким образом, если объем капиталовложений составит 39,2 млн. руб., то ожидаемый объем выпуска продукции составит около 48 млн. руб.

Зададим доверительную вероятность и построим доверительный прогнозный интервал для среднего значения Y.

Для этого нужно рассчитать стандартную ошибку прогнозирования:

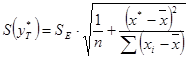
Предварительно подготовим:

- стандартную ошибку модели (Таблица 2);

- по столбцу исходных данных Х найдем среднее значение (функция СРЗНАЧ) и определим (функция КВАДРОТКЛ).

Следовательно, стандартная ошибка прогнозирования для среднего значения составляет:

При размах доверительного интервала для среднего значения

Границами прогнозного интервала будут

Таким образом, с надежностью 90% можно утверждать, что если объем капиталовложений составит 39,2 млн. руб., то ожидаемый объем выпуска продукции будет от 45,3 млн. руб. до 50,67 млн. руб.

7. Представить графически фактические и модальные значения Y точки прогноза.

 Скачать реферат