Методы решения уравнений линейной регрессии

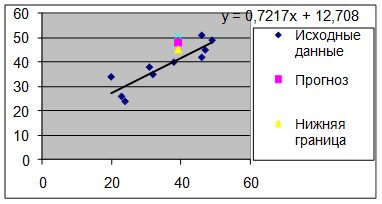
Для построения чертежа используем Мастер диаграмм (точечная) – покажем исходные данные (поле корреляции).

Затем с помощью опции Добавить линию тренда… построим линию модели:

тип → линейная; параметры → показывать уравнение на диаграмме.

Покажем на графике результаты прогнозирования. Для этого в опции Исходные данные добавим ряды:

Имя → прогноз; значения dth=56 height=21 src="images/referats/9820/image070.png">; значения ;

Имя → нижняя граница; значения ; значения ;

Имя → верхняя граница; значения ; значения

8. Составить уравнения нелинейной регрессии: гиперболической; степенной; показательной.

8.1 Гиперболическая модель

Уравнение гиперболической функции:

= a + b/x.

Произведем линеаризацию модели путем замены X = 1/x. В результате получим линейное уравнение

= a + bX.

Рассчитаем параметры уравнения по данным таблицы 2.

b ==

а = =38,4+704,48*0,03=60,25.

Получим следующее уравнение гиперболической модели:

= 60,25-704,48/х.

8.2 Степенная модель

Уравнение степенной модели имеет вид: =аxb

Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:

lg = lg a + b lg x.

Обозначим через

Y=lg , X=lg x, A=lg a.

Тогда уравнение примет вид: Y = A + bX – линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы 3.

b = =

A = = 1,57-0,64*1,53=0,59

Уравнение регрессии будет иметь вид: Y = 0,59+0,64* Х.

Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения.

= 100,59* х0,64.

Получим уравнение степенной модели регрессии:

= 3,87* х0,64.

8.3 Показательная модель

Уравнение показательной кривой: =abx.

Для построения этой модели необходимо произвести линеаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения:

lg = lg a + x lg b.

Обозначим: Y = lg , B = lg b, A = lg a. Получим линейное уравнение регрессии: Y = A + B x. Рассчитаем его параметры, используя данные таблицы 4.

В ==

А == 1,57-0,01*35,6=1,27

Уравнение будет иметь вид: Y = 1,27+0,01х.

Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения:

=101,27* ( 100,01)х = 18,55*1,02х.

Графики построенных моделей:

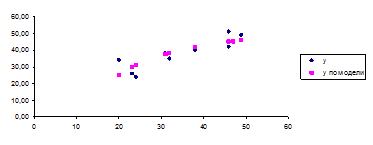
Рис.3. Гиперболическая

Рис.4. Степенная

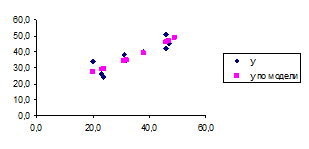
Рис.5. Показательная

9. Сравнение моделей по характеристикам: коэффициенты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Вывод.

9.1 Гиперболическая модель

Коэффициент детерминации:

=

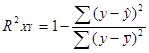Вариация результата Y на 70,9% объясняется вариацией фактора Х.

Коэффициент эластичности:

== 0,05.

Это означает, что при увеличении фактора Х на 1 % результирующий показатель изменится на 0,05 %.

Бета-коэффициент:

Sx==0,01 Sy==8,5 60,25*0,01/8,5=0,07.

Т.е. увеличение объема капиталовложений на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего значения объема выпуска продукции на 0,07 среднеквадратического отклонения этого показателя.

Средняя относительная ошибка аппроксимации:

отн = 109,7/ 10= 10,97 %.

В среднем расчетные значения для гиперболической модели отличаются от фактических значений на 10,97%.

9.2 Степенная модель

Коэффициент детерминации:

=

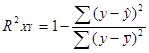Вариация результата Y на 73,6% объясняется вариацией фактора Х. Коэффициент эластичности:

== 0,57.

Это означает, что при увеличении факторного признака на 1 % результирующий показатель увеличится на 0,57%.

Бета-коэффициент:

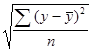, Sy=и Sx=.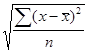

Sx==0,14 Sy==0,10 0,59*0,14/0,1=0,78.

Т.е. увеличение объема капиталовложений на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего значения объема выпуска продукции на 0,78 среднеквадратического отклонения этого показателя.

 Скачать реферат