Информационные технологии сетевого планирования в управлении

Математически условия задачи можно записать следующим образом

(3.1)

(3.2)

(3.3)

(3.4)

c="images/referats/9845/image076.png">; (3.5)

(3.6)

Добавив при необходимости фиктивную операцию, выходящую из последнего события, целевую функцию любого графика можно записать в виде выражения (3.1).

Ограничения-равенства (3.4) показывают зависимость продолжительности выполнения операций от вложенных средств. Ограничения (3.5) обеспечивают выполнение условий предшествования операций в соответствии с топологией сети (время начала выполнения каждой операции должно быть не меньше времени окончания непосредственно предшествующей ей операции).

Критический путь в данной задаче является функцией от объемов дополнительно вкладываемых средств .

Сформулированная задача относится к классу оптимизационных задач и может быть решена методами линейной или нелинейной оптимизации в зависимости от вида функций

Приведем пример решения задачи оптимизации комплекса операций по времени путем затрат дополнительных средств.

Пример 1.

Комплекс операций представлен сетевым графиком (рис. 3.6). Цифры, приписанные дугам, означают соответственно продолжительность и минимально возможное время выполнения операций (в днях).

Продолжительность выполнения операций зависит линейно от дополнительно вложенных средств и выражается соотношением

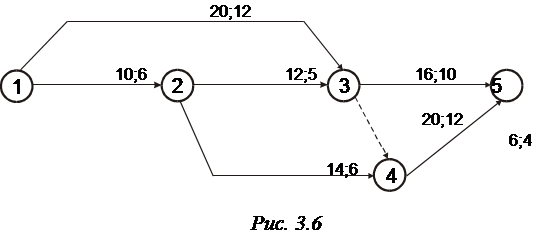
Требуется оптимизировать сетевой график по времени, т.е. определить время выполнения каждой операции сетевого графика таким образом, чтобы время выполнения комплекса операций было минимальным, а сумма вложенных средств не превышала 15 единиц.

Решение

Добавив на сетевом графике фиктивную операцию (5,6), запишем целевую функцию в виде

Запишем ограничения задачи:

· сумма вложенных средств не должна превышать наличного их количества

· время выполнения каждой операции должно быть не меньше минимально возможного времени

· зависимость продолжительностей операций от вложенных средств дает ограничения-равенства

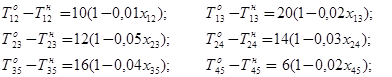
· время начала выполнения каждой операции должно быть не меньше времени окончания непосредственно предшествующей ей операции (моменты времени

· условие неотрицательности неизвестных

для всех дуг сетевого графика.

Создадим на рабочем листе Excel форму для ввода данных, необходимых для решения задачи (Рис. 3.7).

Рис. 3.7. Форма для ввода данных примера 1.

Введем обозначения для переменных согласно Рис. 3.7, и отведем под расчетные значения X1-X20 диапазон ячеек A8:T8. Далее, введем формулы для расчета функций-ограничений в соответствии с приводимой ниже таблицей

Целевой ячейкой является O14.

Вызываем Поиск решения и вводим все необходимые ограничения.

Ответ

 Скачать реферат