Информационные технологии сетевого планирования в управлении

Требуется определить интенсивности потоков, при которых суммарная стоимость доставки была бы минимальной, а потребности узлов 4 и 5 были бы удовлетворены.

Решение

Очевидно, задача сводится к минимизации функции:

при ограничениях

,

184 height=27 src="images/referats/9845/image203.png">,

,

,

,

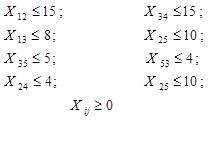
Введем исходные данные на рабочий лист Excel в соответствии с Рис. 3.14. В качестве целевой ячейки выберем E13; для расчетных значений неизвестных интенсивностей потока выделим диапазон ячеек A6:I6. В ячейки A8:A12 и целевую ячейку введем формулы для ограничений задачи и целевой функции в соответствии с приведенной ниже таблицей.

Рис. 3.14 Форма для решения примера 4

После вызова Поиска решения введем следующие ограничения:

В результате решения получим ответ:

и для интенсивностей дуговых потоков

Пример 5

Рассмотрим еще один пример решения задач подобного типа.

Имеется транспортная система, представленная сетевой моделью следующего вида (Рис.3.15). Цифры у дуг означают удельные стоимости перевозки по дугам, соединяющим соответствующие узлы. Требуется определить маршрут, стоимость которого была бы минимальна.

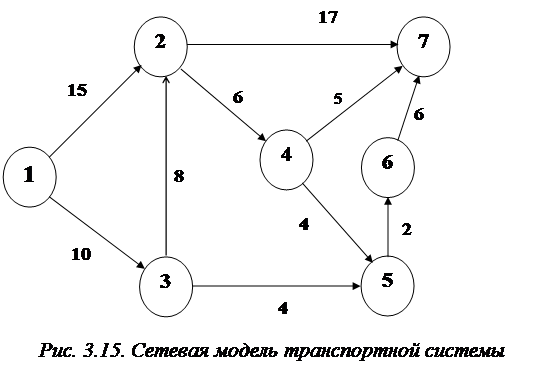Решение. Введем данные на рабочий лист в соответствии с Рис.3.16.

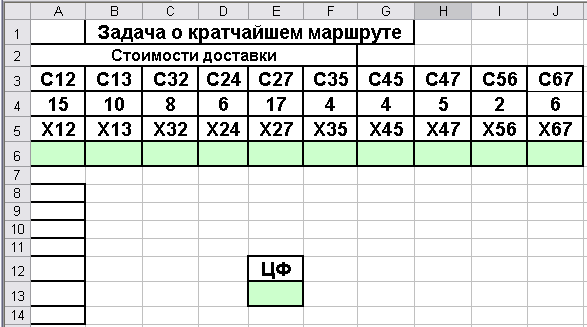
Рис. 3.16 Форма для решения примера 5

Введем следующие формулы в указанные ячейки:

Введем все необходимые ограничения. С помощью Поиска решения получим ответ

Маршрут, перевозка по которому имеет наименьшую стоимость, есть: (1-3-5-6-7).

Задача о кратчайшем маршруте

Рассмотрим задачу определения кратчайшего пути между двумя вершинами сети. Эта задача является частным случаем задачи об оптимальном потоке. Она охватывает широкий круг важных приложений моделей исследования операций (замена оборудования, календарное планирование и др.).

Пусть задана сеть , каждой дуге (ребру) которой соответствует некоторое расстояние . Требуется найти кратчайший маршрут из источника в сток .

Математическая постановка задачи имеет вид: минимизировать

при ограничениях

Приведем пример решения подобной задачи с помощью Microsoft Excel.

Пример 6

Транспортная система представлена схематически на Рис. 3.17. Расстояния между узлами сети указаны у соответствующих дуг (масштаб не соответствует реальным расстояниям). Требуется определить кратчайший (по расстоянию) маршрут между узлами 1 и 7.

 Скачать реферат