Экспертные оценки в управлении

(6.14)

Полагая , получим первое приближение:

где в правой части после умножения на получается некоторый вектор . После нормировки он представляется в виде

где - нормирующая константа, - нормированный вектор (т.е. вектор, сумма составляющих которого равна единице).

Определив , подставим его в правую часть уравнения (3.14) и повторяем вычисления.

Как правило, итерационный процесс продолжается до тех пор, пока величины - го приближения не будут отличаться от соответствующих величин -го приближения не более, чем на (обычно принимают ). Скорость сходимости итерационного процесса зависит от выбора начального приближения. Часто в качестве выбирают первый столбец матрицы .

Пример. Для матрицы попарного сравнения

вычислим с помощью итерационной процедуры максимальное собственное число и соответствующий ему собственный вектор. В качестве начального приближения возьмем первый столбец матрицы. Получим

Суммируя составляющие, найдем первое приближение для максимального собственного числа

.

Тогда

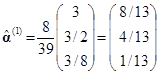
Вычисляя второе приближение, получим

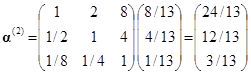
Суммируя компоненты этого вектора, получим

Поэтому

Дальнейшие вычисления не меняют результат.

Приведем пример расчета в Excel матрицы попарных сравнений в случае несогласованной исходной матрицы.

Пример 2.

Исходная матрица попарных сравнений имеет вид

Легко убедиться в том, что данная матрица не является согласованной.

Введем расчетные формулы в соответствии с Рис. 6.3. Как и в предыдущем примере, итерационный расчет будем проводить при использовании в качестве начального приближения первого столбца исходной матрицы попарных сравнений.

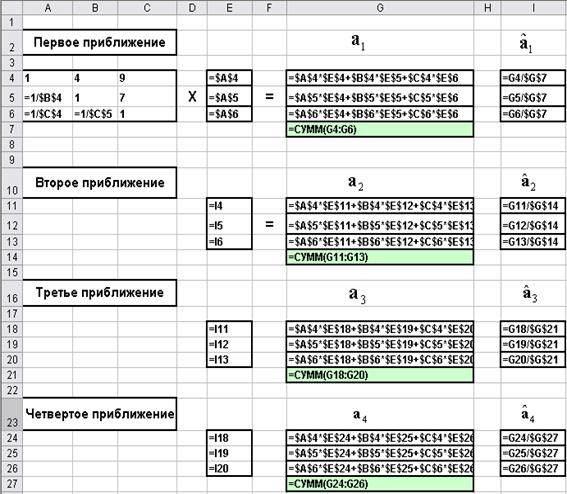
Рис. 6.3 Формулы и исходные данные для решения примера 2

Расчет показывает (см. ниже), что в данном случае согласованные результаты получаются (с достаточно высокой точностью) уже после 2-3 итераций. После четвертой итерации результаты практически не изменяются. Таким образом, данный простейший алгоритм позволяет существенно упростить процедуру расчета матрицы попарных сравнений в случае, когда исходная матрица является несогласованной.

Результаты расчетов для случая несогласованной исходной матрицы попарных сравнений

 Скачать реферат