Некоторые задачи оптимизации в экономике

F=CX→ min (max)

AX=B, X≥0

2 вид – векторная форма записи:

F=CX→ min (max)

р1x1+р2x2+…+рnxn=р. Х≥0.

р1= р2= … р n=.

Для того чтобы рассмотреть теоретические основы метода линейного программирования, определим понятие выпуклого множества точек, дав ему определение в аналитической форме:

Множество точек является выпуклым, если оно вместе с любыми своими двумя точками содержит их произвольную линейную комбинацию. Точка Х является выпуклой линейной комбинацией точек Х1, Х2, … Хn, если выполняются условия Х= α1x1+α2x2+…+αnxn, αj≥0, (j=1,…,n), .

Теорема 1. Выпуклый линейный многогранник является выпуклой линейной комбинацией своих угловых точек. (Примем без доказательства).

Теорема 2. Множество всех допустимых решений системы ограничений ЗЛП является выпуклым.

□ Пусть Х1=( x,x, …,х) и Х2=( x,x, …,х)- два допустимых решения задачи (3.3), заданной в матричной форме. Тогда АХ1=В и АХ2=В. рассмотрим выпуклую линейную комбинацию решений Х1 и Х2 , т.е. Х=α1Х1+α2Х2 при α1 ≥0, α2 ≥0 и α1+α2=1. Покажем, что она также является допустимым решением системы АХ=В. В самом деле, АХ=А(α1Х1+α2Х2)=α1АХ1+(1-α1)АХ2= α1В+(1-α1)В=В, т.е. решение удовлетворяет системе ограничений. Но т.к. Х1≥0, Х2 ≥0, α1 ≥0, α2 ≥0 , то и Х ≥0, т.е. решение Х удовлетворяет условию (3.3). ■

Итак, доказано, что множество всех допустимых решений ЗЛП является выпуклым, которое будем называть многогранником решений.

Ответ на вопрос, в какой точке многогранника решений возможно оптимальное решение ЗЛП, даёт следующая теорема.

Теорема 3. Если ЗЛП имеет оптимальное решение, то линейная функция F принимает максимальное (минимальное) значение в одной из угловых точек многогранника решений. Если линейная функция принимает максимальное значение более чем в одной угловой точке, то она принимает его в произвольной точке, являющейся выпуклой линейной комбинацией этих точек.

□ Будем полагать, что многогранник решений является ограниченным. Обозначим его угловые точки через Х1,Х2, …,Хn , а оптимальное решение через Х*. Тогда F(Х*) ≥F(X), для всех точек многогранника решений. Если Х* угловая, то первая часть теоремы доказана. Предположим, что Х* не является угловой точкой, тогда Х*, на основании теоремы 1, можно представить как выпуклую линейную комбинацию угловых точек многогранника решений, т.е. Х*=α1x1+α2x2+…+αрxр, αj≥0, (j=1,…,n), . Т.к.

F(Х*)=F(α1x1+α2x2+…+αрxр)=α1F(x1)+α2F(x2)+…+αрF(xр). (3.4)

В этом выражении среди значений F(Xj)(j=1,2,…,p) выберем максимальное. Обозначим его через М, т.е. М=max F(Xj). Тогда

α1F(x1)+ α2F(x2) +…+ αрF(xр)≤ α1М+ α2М +…+ αрМ = М(α1+α2+…+αр) =М.

Значит F(Х*)≤М. Пусть М=F(Xk), т.е. соответствует угловой точке Xk (1≤к≤р).

Тогда F(Х*) ≤ F(Xk). Но по предположению Х* - оптимальное решение, поэтому F(Х*)≥F(Xk)=М, следовательно, F(Х*)=М=F(Xk), где Xk- угловая точка. Итак, существует угловая точка Xk, в которой линейная функция принимает максимальное значение.

Для доказательства второй части теоремы допустим, что F(Х) принимает максимальное значение более чем в одной угловой точке, например в точках Х1, Х2, … Хq , где 1≤ q ≤ р; тогда F(Х1)=F(Х2)=…=F(Хn)=M.

Пусть Х выпуклая линейная комбинация этих угловых точек, т.е. Х= α1Х1+α2Х2+ …+αqХq , αj≥0, (j=1,…,q), . В этом случае, учитывая, что функция F(Х) – линейная, получим F(Х)=F(α1Х1+α2Х2+…+αqХq)=α1F(Х1)+ +α2F(Х2)+…+αqF(Хq)=α1M+α2M+…+αqM=M=M, т.е. линейная функция F принимает максимальное значение в произвольной точке Х, являющейся выпуклой линейной комбинацией угловых точек Х1, Х2, … Хq ■

Замечание. Требование ограниченности многогранника решений в теореме является существенным, т.к. в случае неограниченной многогранной области не каждую точку можно представить выпуклой линейной комбинацией её угловых точек.

Доказанная теорема является фундаментальной, т.к. она указывает принципиальный путь решения ЗЛП.

Рассмотрим геометрический метод решения ЗЛП в случае функции двух переменных.

Было доказано, что оптимальное решение ЗЛП находится, по крайней мере, в одной из угловых точек многогранника решений.

Рассмотрим задачу в стандартной форме с двумя переменными.

F=c1x1+c2x2+с0 →min(max),

При ограничениях а11х1+ а12х2 ≤b1,

а21х1+ а22х2 ≤b2,

………………

an1х1+ аn2х2≤bn ,

при условии, что x1 ≥0 ,x2 ≥0 .

Пусть геометрическим изображением системы ограничений является многоугольник ABCDE. Необходимо среди точек этого многоугольника найти такую точку, в которой линейная функция F=c1x1+c2x2+с0 принимает максимальное (или минимальное) значение. Рассмотрим линии уровня функции F или

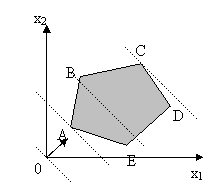c1x1+c2x2=С ( 3.5).

Это уравнение прямой. Линии уровня функции F параллельны, т.к. их угловые коэффициенты определяются только соотношением между коэффициентами c1 и c2 и, следовательно, равны. Т.о., линии уровня функции F – это своеобразные «параллели», расположенные обычно под углом к осям координат.

Важное свойство линий уровня линейной функции состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в другую сторону – только убывает. При фиксированном С рассмотрим линейную функцию. Чем больше значение С, тем больше значение линейной функции. Определив направление возрастания линейной функции, найдём точку, принадлежащую многоугольнику, в которой функция принимает максимальное или минимальное значение.

Геометрическим изображением системы ограничений может служить и многоугольная область. Рассмотрим следующую задачу.

 Скачать реферат